An alternate MST algorithm¶
Prim's algorithm does a graph search while computing the MST.
Can we just greedily add edges in increasing order of weight?
Almost: need to avoid cycles and ensure we "span" the graph
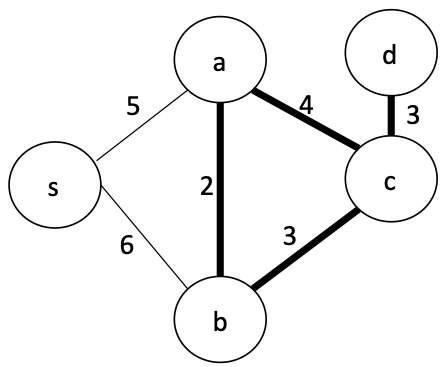
Kruskal's Algorithm¶
“Perform the following step as many times as possible: Among the edges of $G$ not yet chosen, choose the shortest edge which does not form any loops with those edges already chosen.” [Kruskal, 1956]
Why is this correct?
Recall the Light-edge property
Let $G = (V,E,w)$ be a connected undirected, weighted graph with distinct edge weights.
For any cut of $G$, the minimum weight edge that crosses the cut is contained in the minimum spanning tree of $G$.
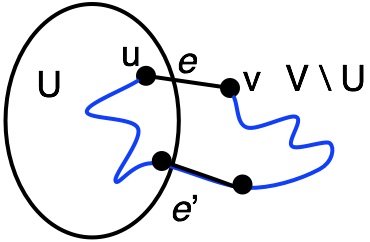
At each step, Kruskal picks a light edge to connect components of the graph $U$ and $V$ (i.e., picks an edge $e$ where $w(e) < w(e')$).
How do we know the tree spans all the nodes?
The only edges we've skipped are those that create a cycle, so the remaining edges must form a tree.
Implementing Kruskal's algorithm¶
"choose the shortest edge which does not form any loops with those edges already chosen"
How do we implement this?
For an edge $(u,v)$, we must check if $u$ and $v$ are in the same connected component, based on the edges added so far.
How can we do this?
If we think of each connected component as a set of nodes, we need an efficient way of:
- checking which set $u$ and $v$ are in
- determining if these two sets are equal
- if they are not equal, then we need to take their union
Using sets to implement Kruskal's¶
To make checking set equality fast, we will assign a representative node in each set.
E.g., suppose we have two sets $\mathbf{S} = \{S_1, S_2\}$ where:
$S_1 = \{\mathbf{a},b,c\}~~~~ S_2 = \{\mathbf{s}, d, e\}$
We can (arbitrarily) assign the representative of $S_1$ to be $a$, and the representative of $S_2$ to be $s$.
$r(S_1) = a ~~~ r(S_2) = s$
If $S_u$ is the set containing $u$ and $S_v$ is the set containing $v$, then we can check if $u$ and $v$ are in the same set by checking if $r(S_u) == r(S_v)$
Disjoint-set data type¶
We have described a disjoint-set abstract data type (aka union-find). This type supports three operations:
make_set(u): create a new set containing the single element $u$- $u$ will be the representative of this set
find_set(u): returns the representative of the set containing $u$: $r(S_u)$
union(u,v): replace $S_u$ and $S_v$ with $S_u \cup S_v$ in the collection of sets $\mathbf{S}$
What data structures can we use to represent each set?
Disjoint-set with double linked lists¶

Each set is a doubly-linked list. The first node is the representative.
How can we perform the three operations and what is the work?
make_set(u): create a new set containing the single element $u$- $u$ will be the representative of this set
find_set(u): returns the representative of the set containing $u$: $r(S_u)$
union(u,v): replace $S_u$ and $S_v$ with $S_u \cup S_v$ in the collection of sets $\mathbf{S}$
make_set(u): create a singleton list in $O(1)$ time. $u$ is the representative.
find_set(u): walk left from $u$ until the first element is found: $O(n)$
union(u,v): Connect the tail $S_u$ to the head of $S_v$: $O(1)$
That's a lot of needless walking. Can I just store the representative directly at each node?
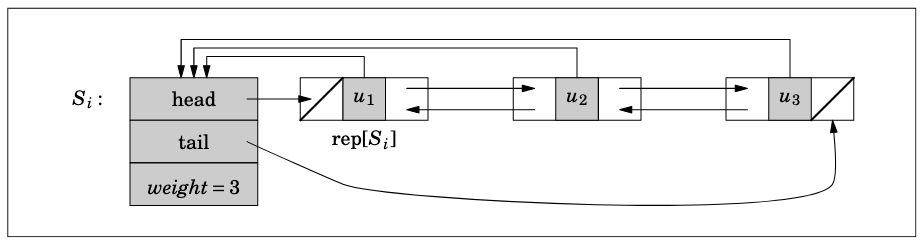
This would make find_set(u) in $O(1)$, but now union becomes $O(n)$. Why?
Disjoint-set with balanced forests¶
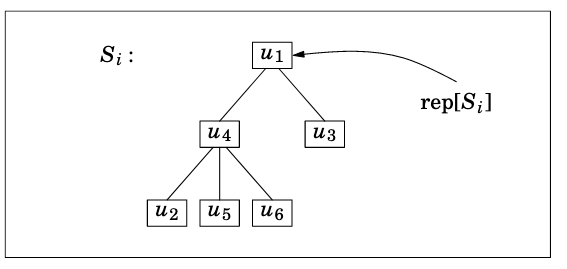
Each set is a balanced tree, where the root is the representative.
Assuming we represent a tree node with a pointer to its parent, what is the work of find_set(u) (to find the representative of $S_u$?
$O(\log n)$, assuming a balanced tree, to walk from a node to its root.
How about union(u,v)?
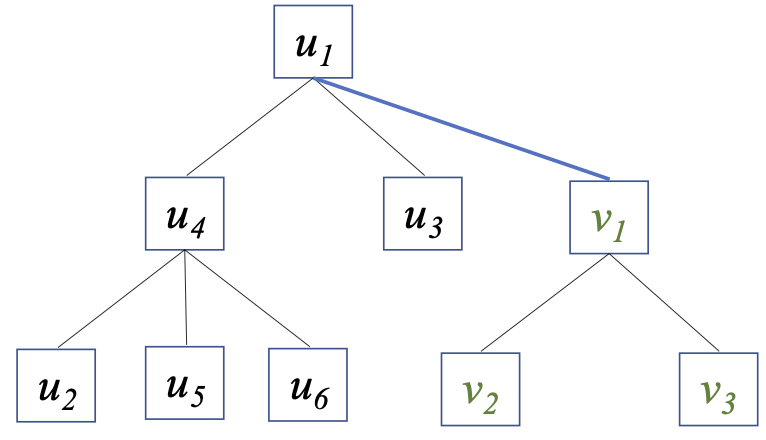
- find representative of $u ~~~~ O(\log n)$
- find representative of $v ~~~~ O(\log n)$
- link root of one tree to the root of another
But, how do we ensure tree stays balanced to keep $O(\log n)$ work for find_set(u)?
Recall Leftist Heaps from Greedy module!
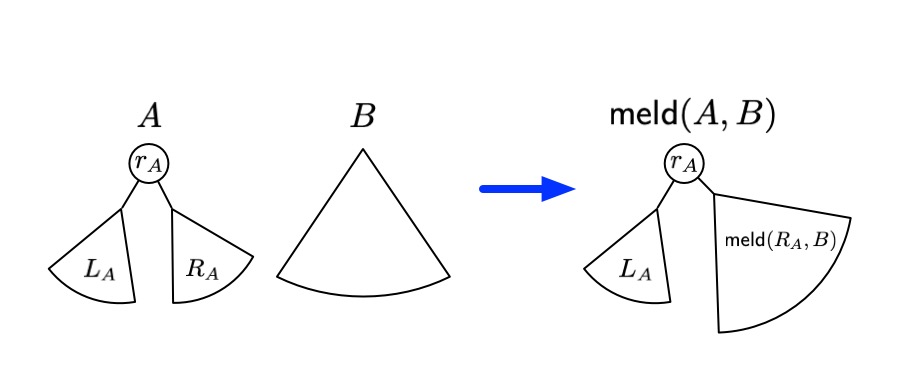
similar idea here:
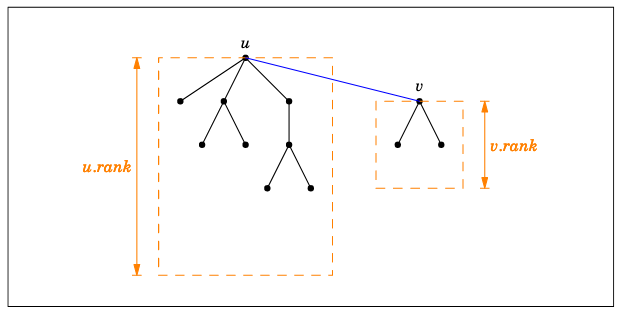
Add "shorter" tree to the "taller" tree.
- store the "rank" of each tree as its depth
Thus, if $height(S_v) < height(S_u)$, then the height the union of $S_u \cup S_v$ is
$\max \{ height(S_u), height(S_v)+1\}$
Using similar arguments as in leftist heaps, we can ensure that height of any tree is $O(\log n)$
Kruskal's Algorithm¶
Initialize tree $T \leftarrow \emptyset$
For each $v \in V$, run
make_set(v)Sort edges in increasing order of weight
For each edge $e=(u,v)$ in sorted set:
- if
find_set(u)$\ne$find_set(v):- $T \leftarrow T \cup \{(u,v)\}$
union(u,v)
- if
Kruskal's Algorithm - work¶
Initialize tree $T \leftarrow \emptyset$
- $O(1)$
For each $v \in V$, run
make_set(v)- $O(|V|)$
Sort edges in increasing order of weight
- $O(|E|\lg |E|)$
For each edge $e=(u,v)$ in sorted set: $O(|E|)$
- if
find_set(u)$\ne$find_set(v): $O(\lg |V|)$- $T \leftarrow T \cup \{(u,v)\}$
union(u,v)
- Together: $O(|E|\lg |V|)$
- if
Thus, total work is $O(|E|\lg |E|)$
Since we have $E \in O(|V|^2)$, this is equivalent to:
$O(|E|\lg |V|^2) \equiv O(2|E| \log |V|) \equiv O(|E| \log |V|)$
Traveling Salesperson Problem¶
Consider a slight variant of the MST problem:
Given a graph $G=(V,E)$, find a tour that visits each node exactly once and then returns to the origin node.
- every node is visited
- no edges are repeated

Often, we assume the graph is complete (fully connected) and edge weights are distance between each city.
How does this differ from the MST problem?
- TSP solution has one more edge than MST solution (graph instead of a tree)
- Therefore, weight(MST solution) < weight(TSP solution)
Thus, MST solution provides a lower bound on the TSP solution.
Can we also use MST to find an upper bound?
Euclidean TSP¶
Variant of TSP where triangle inequality holds:
$w(u,v) + w(v,w) \ge w(u,w)$
where all weights are non-negative.
Consider a MST solution for the graph:
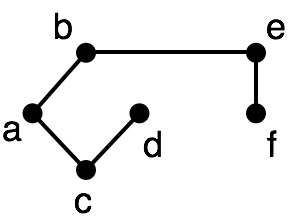
How could we convert this tree into a tour for TSP?
We need to determine an order to visit the nodes in the MST solution.
Let's try depth-first search:
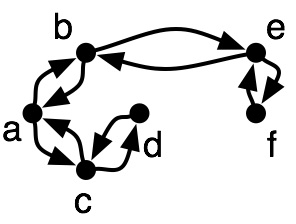
This is called the Euler tour of the tree:
- a cycle in a graph that visits every edge exactly once.
- We view each undirected edge as two directed edges, one for each direction
- Since $T$ spans the graph, the Euler tour will visit every vertex at least once, but possibly multiple times.

This is close to a TSP solution, but:
it visits each edge twice
$(d,f)$ should have an edge
The weight of the Euler tour is equal to twice the MST weight (since we visit each edge twice).
How can we convert this to a proper solution to TSP?
idea:
Compute DFS order, but when we find a repeated edge, instead find the next unvisited vertex.
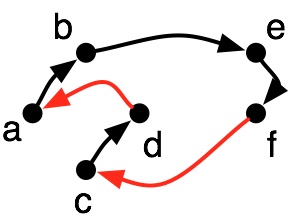
The red edges above are called shortcut edges.
Because of triangle inequality, we know that the shortcut edges are no longer than the paths they replace
$w(f,c) \le w(\langle f,e,b,a,c \rangle)$
Since we know:
$weight(MST) < weight(TSP)$
$weight(Euler) = 2 \cdot weight(MST)$
then we know
- $weight(MST) \le weight(TSP) \le 2 \cdot weight(MST)$