Agenda:
- Priority Queues/Heap
We saw two greedy algorithms that both construct the solution by evaluating a greedy choice. But how do we easily identify the choice?
Often times, we can sort the solution choices by our greedy criterion. But this only works if we don't need to recompute the criterion each time we change the solution.
The priority queue is a tree-based data structure that works well with greedy algorithms since it allows for efficient insertions, removals, and updates of items.
Priority Queues¶
For simplicity we'll assume that we are always seeking the minimum-value element from the priority queue. The priority queue ADT needs to support some basic operations:
deleteMin: Identify the element with minimum value and remove it.
insert(x, s): insert a new element $x$ with initial value $s$.
Note that for the static case in which scores don't change, sorting took $O(n\log n)$ work and $O(\log^2 n)$ span.
This suggests that we should aim for $O(\log n)$ work per operation.
The Heap Property¶
The heap property for a tree states that every node in the tree is smaller than either of its children. This means that the root of a tree with the heap property is always the minimum element. So for a binary tree:
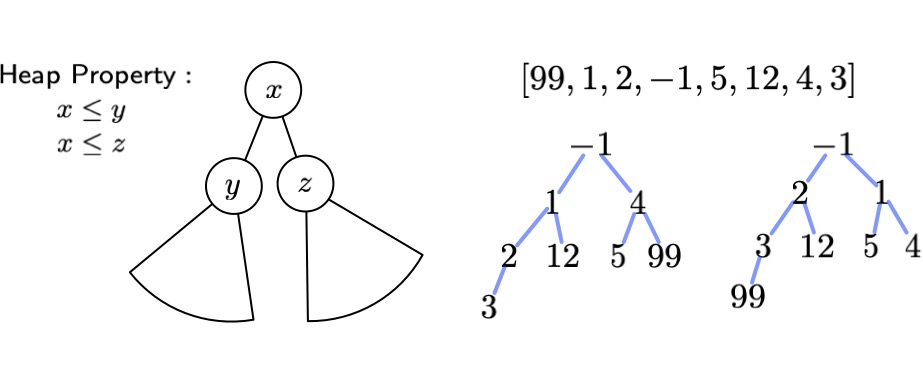
We've seen that binary trees that have all possible nodes have logarithmic depth. In lab you will implement a binary heap, which has optimal performance since it is an "almost-complete", and thus balanced, binary tree.
Maintaining the heap property upon insertion or deletion will require time proportional to the depth of the tree because we can swap elements upward or downward, following the path from the modification either upward or downward.
Meldable Heaps¶
We'll look at a BST alterntaive to maintaining the shape property. We will maintain the heap property, but will not require our trees to be almost-complete.
We will make use of the observation that really, heap operations just require the ability to combine or meld heaps efficiently:
- deleteMin needs to delete the root of the tree, and then somehow meld the left and right subtrees.
- to delete the minimum value, remove the root and meld the two subtrees
- insert is just the melding of the current tree and and a singleton tree.
- With the meld operation, we can construct a priorty queue in parallel: $\texttt{val pq = Seq.reduce Q.meld Q.empty (Seq.map Q.singleton S)}$
How to Meld¶
Suppose we wish to meld two heaps $A$ and $B$, with $A$ smaller than $B$.
To meld $A$ and $B$ into a single tree $C$, we need to pick one of them to be the root of $C$.
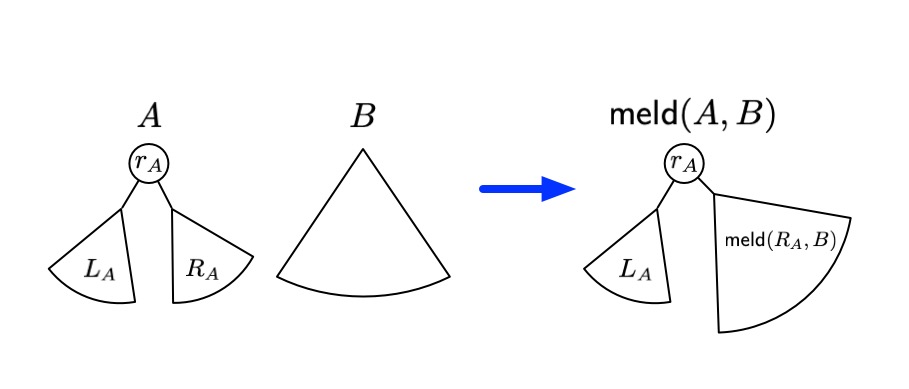
Suppose we let the root $r_A$ of the smaller tree $A$ be the new root.
If we maintain the left subtree $L_A$ of $r_A$, we can meld $R_A$ and $B$ and make this the right subtree of $r_A$.
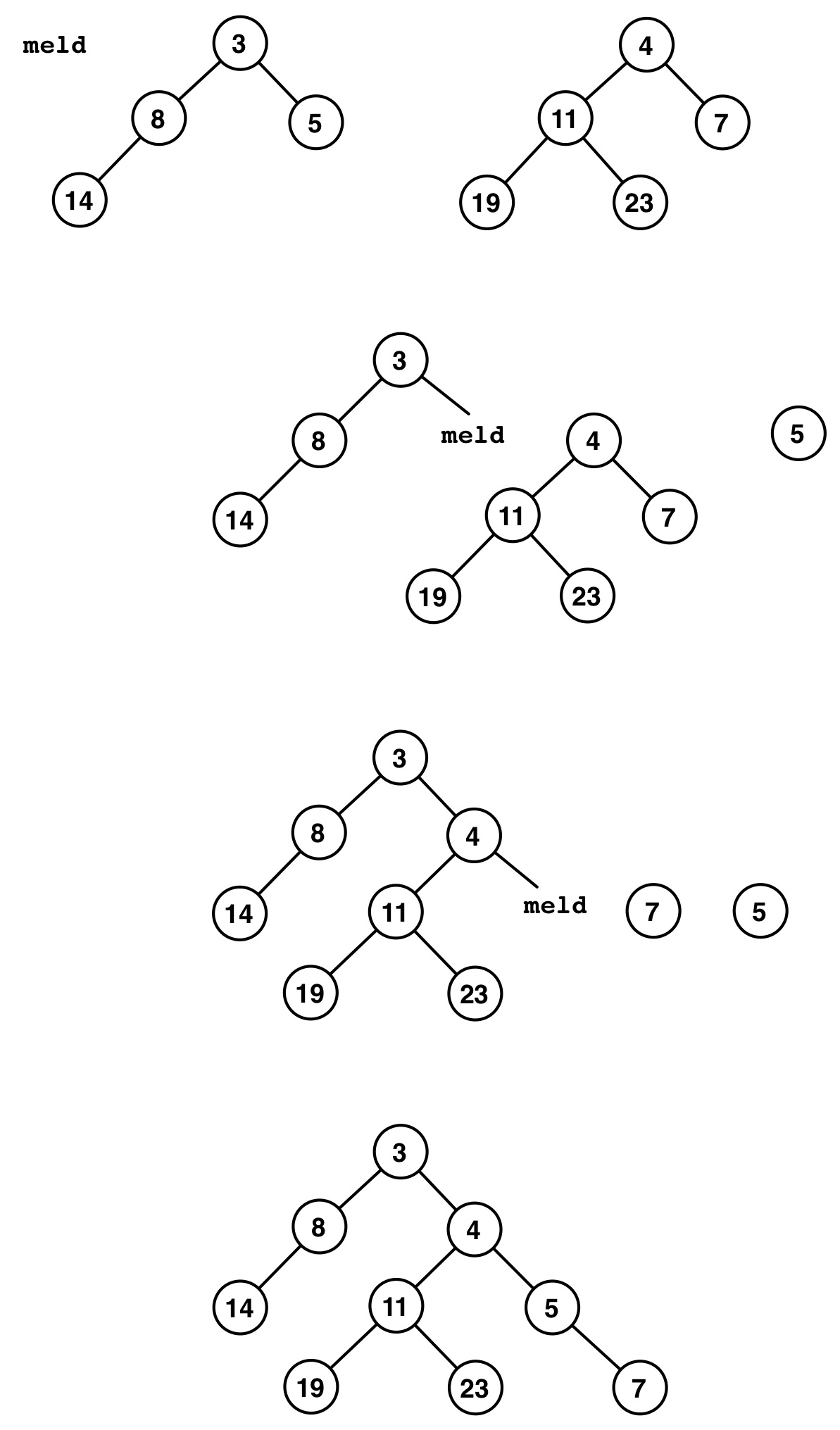
This defines a recursive procedure for melding two heaps:
This is a well-defined procedure for melding two heaps, but it is possible to obtain a very long right "spine" of the melded tree. Actually in the worst case we might take $\Theta(|A|+|B|)$ work!

Leftist Heaps¶
To address this imbalance in our approach, we can do some bookkeeping and use our flexibility in choosing how to orient subtrees left to right.
We will ensure that the tree is always deeper on the left than the right.
The right spine of a binary tree is the path from the root to the rightmost node.
Let $rank(x)$ be length of the right spine starting at $x$.
Let $L(x)$ be the left child of $x$ and $R(x)$ the right child of $x$.
A leftist heap has the property that for any node $x$ in the heap: $rank(L(x)) \geq rank(R(x))$.
Of course, a leftist heap could be imbalanced on the left:
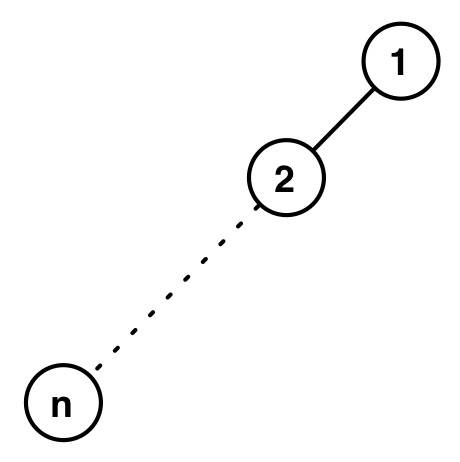
Why is this ok?
Meld only traverses the right spine of a tree.
Fortunately, maintaining the leftish property is simple.
The $rank$ measure allows us to enforce the leftish property.
The key idea is that after melding into the right subtree, if the resulting tree has a higher rank than the left subtree, swap them.
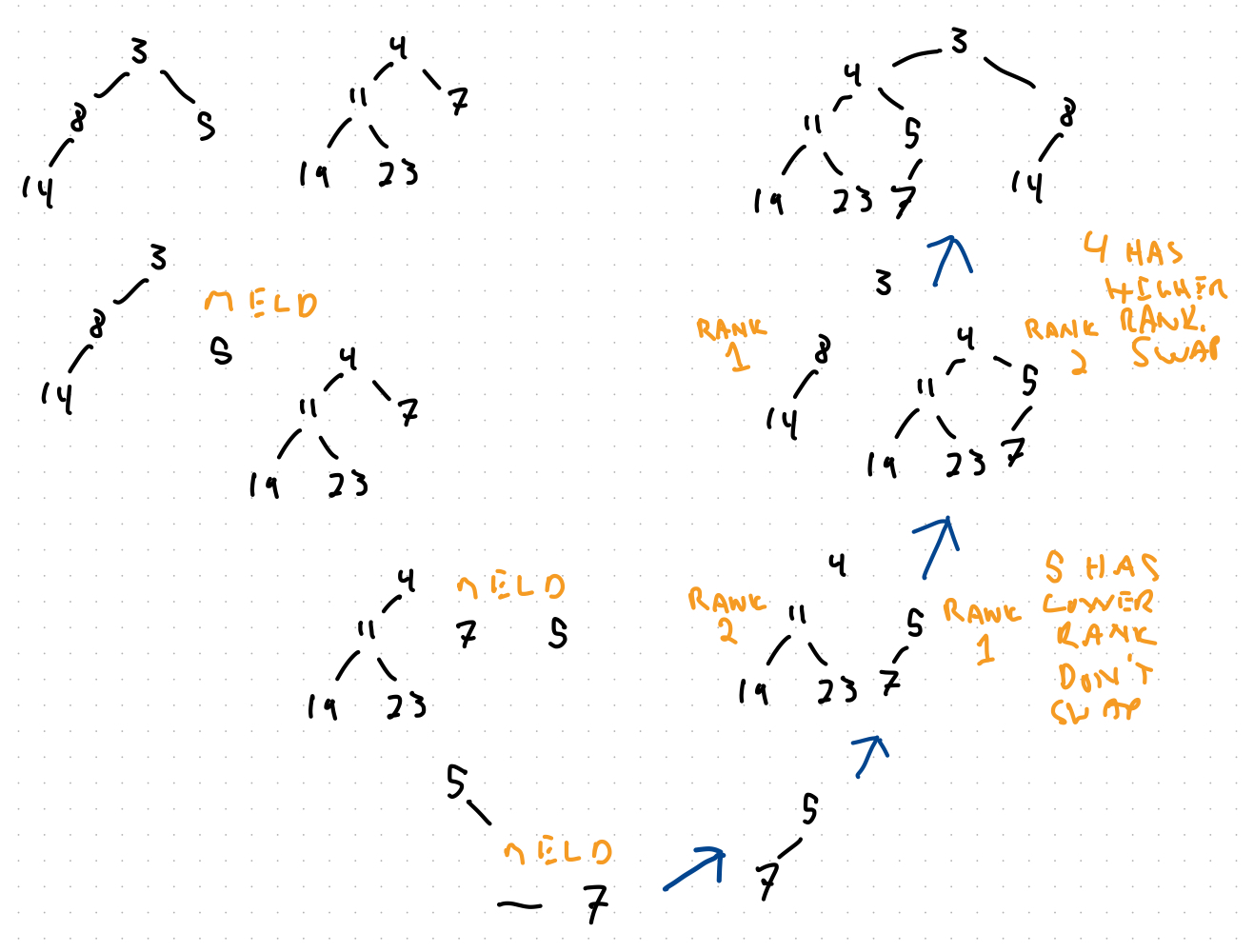

Leftist Heap Recap¶
- Leftist heaps depend on the meld operation for deleteMin and insert.
meld combines two heaps by recursively melding one into the right subheap of the other.
- meld recursively operates down the right spine to build the melded heap
- To keep meld efficient, a leftist heap keeps the right spine of the heap short by ensuring that every meld maintains the invariant:
- $rank(R(x)) \leq rank(L(x))$
Does this guarantee logarithmic runtimes?
Theorem: If $A$ and $B$ are leftist heaps, then meld runs in $O(\log |A| + \log |B|)$ work.
The key observation is that the meld operation only advances along the right spine of either $A$ or $B$.
The number of recursive calls will be limited by $rank(A)$ or $rank(B)$.
What is the relationship betweent the size of a leftist heap and its rank?
Lemma: In a leftist heap with $n$ nodes, the rank of the root node is at most $\log_2 (n + 1).$
Proof: To prove this lemma, we first want to show that if a heap has rank $r$, then it has at least $2^r - 1$ nodes.
Let $n(r)$ be the number of nodes in the smallest leftist heap of rank $r$. According to the way we assign rank, the right child of any node $x$ of rank $r$ is $r-1$.
Also by the leftist property, for a node $x$ of rank $r$:
$rank(L(x)) \geq rank(R(x)) = r - 1.$
Then for a leftist heap rooted at $x$ of rank $r$ we get the following recurrence:
$n(r) = 1 + n(rank(L(x))) + n(rank(R(x)))$
$n(r) \geq 1 + n(r-1) + n(r-1)$
$n(r) \geq 1 + 2n(r-1)$
This recurrence yields a complete binary tree which has $n(r) \geq 2^{r}-1$.
Now to prove the lemma, suppose we have a leftist heap with $n$ nodes and rank $r$. First, $n \geq n(r)$ by definition. This means that $n \geq 2^r - 1$.
$$\begin{align} n &\geq 2^r - 1 \\ n + 1 &\geq 2^r \\ r &\leq \log_2 (n+1) ~~ \blacksquare \end{align} $$Theorem: If $A$ and $B$ are leftist heaps, then the meld algorithm runs in $O(\log |A| + \log |B|)$ work.
Proof: Since meld only advances along the right spine of either $A$ or $B$, and since rank decreases by 1 each time we advance, there are $rank(A) + rank(B)$ constant-time operations in total. By the lemma, this results in $O(\log |A| + \log |B|)$ work. $\blacksquare$
Lemma: In a leftist heap with $n$ nodes, the rank of the root node is at most $\log_2 (n + 1).$