Towards parallel MST¶
We know that each light edge must be in the MST.
Prim and Kruskal pick light edges one at a time.
Can we pick more than one at a time?
We know that lowest weight edge from a vertex must be in MST. Call these the vertex-bridges of the graph.
What if, for our MST algorithm, we simply select the smallest edge leaving each vertex?

Are we done?

We haven't necessarily selected $n-1$ edges, which we need to have a MST.
The problem is some edges are selected by multiple vertices -- e.g., $a$ and $b$ both pick edge $(a,b)$.
So, we need to repeat this somehow, efficiently.
If we could collapse together the vertices connected by the selected edges, then we could solve a smaller version of this problem.
This is exactly what contraction is for!
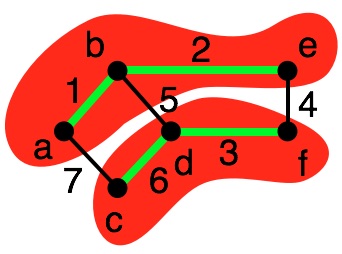
Due to light edge property, we know we should select $(e,f)$ which has minimum weight of $4.$
Notice that by collapsing vertices, we are ignore internal edges -- e.g., if there were an edge from $c$ to $f$, we would ignore it when collapsing $c,d,f$. Why is this okay?
Borůvka's Algorithm¶
While there are edges remaining:
select the minimum weight edge out of each vertex and contract each part defined by these edges into a vertex;
remove internal edges, and when there are redundant edges keep the minimum weight edge; and
add all selected edges to the MST.
We need to:
- figure out the number of iterations
- figure out how to do the contraction
Bounds on contraction¶
How many vertices will we contract at each iteration? Consider the example again:

If a partition has $k$ edges, how many vertices will be removed?
$k$
So, if the graph has $n$ vertices, and we pick one edge per vertex, what is the best and worst case on the number of vertices we can remove at each round?
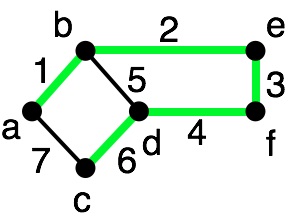
Best-case: contract away $n-1$ vertices. We found the MST in one iteration!
Worst-case: contract away $\frac{n}{2}$ vertices. Each edge removes a single vertex.
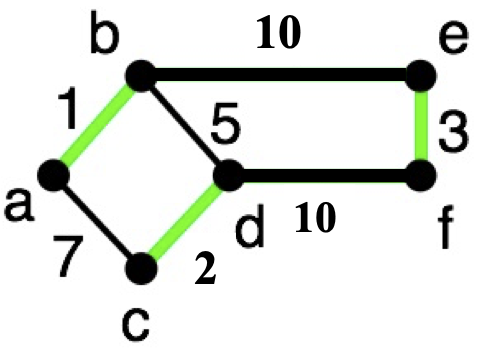
So, we're guaranteed to remove atleast $n/2$ vertices at each iteration.
Total number of contraction iterations is $O(\lg n)$
Contracting in Borůvka's Algorithm¶
How can we contract these partitions?

In the above example, each partition happens to be a star graph, but it won't always be so:

Instead, we can apply star partitioning directly to the subgraph created by the vertex-bridges.
Star partitioning in Borůvka¶
The only difference is that we only contract edges that are vertex bridges:


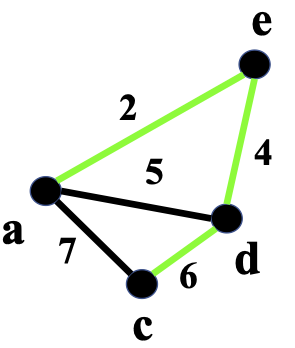
E.g., we didn't contract $(b,d)$ because it is not a vertex bridge.
$ \begin{array}{ll} 1 ~~ \mathit{bridgeStarPartition}~(G=(V,E), i) = \\ 2 ~~ ~~~~\texttt{let} \\ 3 ~~ ~~~~~~~~\mathit{Eb} = \mathit{vertexBridges}~(G) \\ 4 ~~ ~~~~~~~~\mathit{P} = \left\{ u \mapsto (v,w) \in \mathit{Eb} \;|\; ( \mathit{flips}~(u) = T) \land (\mathit{flips}~(v) = H) \right\} \\ 5 ~~ ~~~~~~~~V' = V \setminus \mathit{domain}(P) \\ 6 ~~ ~~~~\texttt{in} \\ 7 ~~ ~~~~~~~~(V',P) \\ 8 ~~ ~~~~\texttt{end} \end{array} $
As in the star contraction lecture, the expected number of vertices removed at each step is $\frac{n}{4}.$
This is is not as good as $\frac{n}{2}$, but still good enough to ensure a logarithmic number of contraction iterations.
Implementing Borůvka's Algorithm¶
While there are edges remaining:
- select the minimum weight edge out of each vertex and contract each part defined by these edges into a vertex;
- Can implement with a min
reduceat each vertex: span $\Rightarrow O(\lg |V|)$.
- Can implement with a min
- remove internal edges, and when there are redundant edges keep the minimum weight edge;
- One run of star contraction: span $\Rightarrow O(\lg |V|)$.
- add all selected edges to the MST.
filter: span $\Rightarrow O(\lg |E|) \in O(\lg |V|)$