Star Graph¶
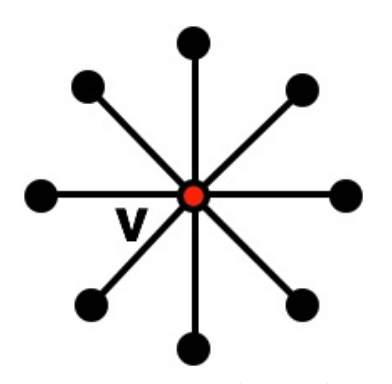
A star graph $G = (V,E)$ is an undirected graph with
- a center vertex $v \in V$, and
- a set of edges $E$ that attach $v$ directly to the rest of the vertices, called satellites , i.e., $E = \left\{ \left\{ v,u \right\} : u \in V \setminus \left\{ v \right\} \right\}$.
How many edges can we contract per iteration using edge contraction?
at most 1 per round, so $n$ iterations
we need $O(\log n)$ iterations to reduce span
Edge contraction generally doesn't work well for graphs with many high degree vertices.
We instead need a way to identify and contract star patterns all at once.
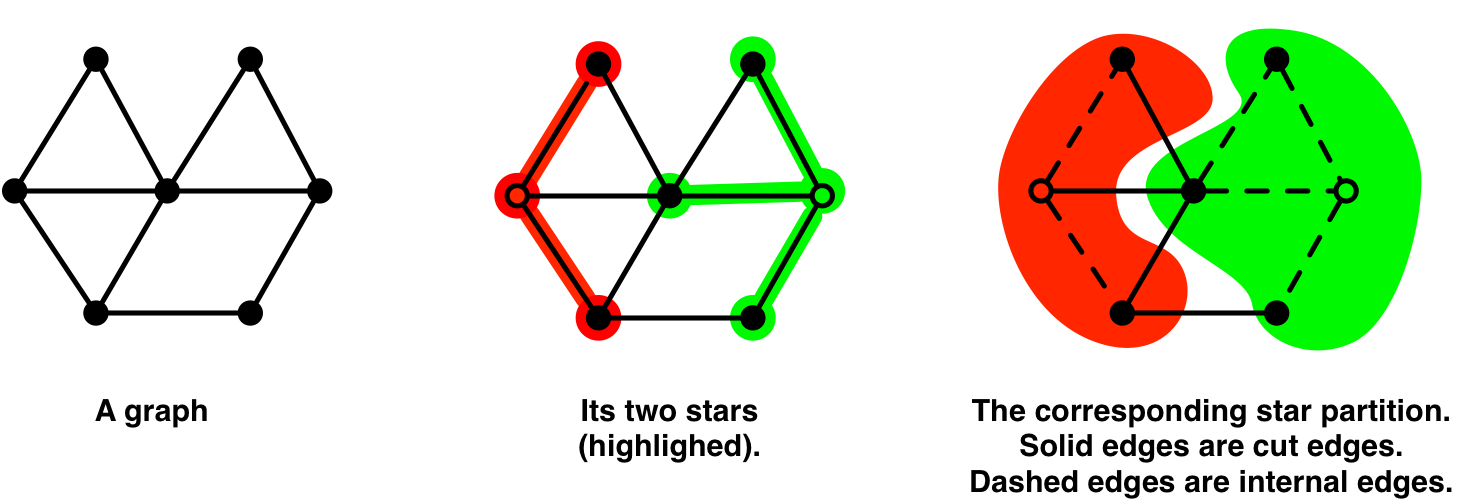
Star Partition¶
A star partition of a graph $G$ is a partition of $G$ where each block is vertex-induced subgraph with respect to a star graph.
How can we identify such stars?
To construct a star partition:
- Select an arbitrary vertex $v$ from the graph and make $v$ the center of a star.
- Attach as satellites all the neighbors of $v$ in the graph.
- Remove $v$ and its satellites from the graph.
But, this is sequential. We want to do it in parallel.
We'll use randomness similar to how we did with edge partitioning.
Parallel star partitioning¶
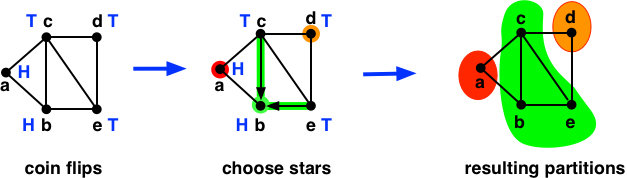
- Flip a coin for each vertex.
- If a vertex flips heads, then it becomes the center of a star.
- If a vertex flips tails, then there are two cases.
- If the vertex has a neighbor that flips heads, the vertex selects the neighbor and becomes a satellite.
- The vertex doesn’t have a neighbor that flips heads. In this case, the vertex becomes a center.
$ \begin{array}{ll} 1 ~~ \mathit{starPartition}~G=(V,E) = \\ 2 ~~ ~~~~\texttt{let} \\ 3 ~~ ~~~~~~~~\texttt{(* Find the arcs from satellites to centers. *)} \\ 4 ~~ ~~~~~~~~\mathit{TH} = \left\{ (u,v) \in E \;|\; \neg (\texttt{heads}~u) \land (\texttt{heads}~v) \right\} \\ 5 ~~ ~~~~~~~~\texttt{(* Partition map: satellites map to centers *)} \\ 6 ~~ ~~~~~~~~P_s = \bigcup_{(u,v) \in \mathit{TH}} \left\{ u \mapsto v \right\} \\ 7 ~~ ~~~~~~~~\texttt{(* Centers are non-satellite vertices *)} \\ 8 ~~ ~~~~~~~~V_c = V \setminus \mathit{domain}(P_s) \\ 9 ~~ ~~~~~~~~\texttt{(* Map centers to themselves *)} \\ 10 ~~ ~~~~~~~P_c = \left\{ u \mapsto u : u \in V_c \right\} \\ 11 ~~ ~~~~\texttt{in} \\ 12 ~~ ~~~~~~~~(V_c, P_s \cup P_c) \\ 13 ~~ ~~~~\texttt{end} \end{array} $

$V = \{a, b, c, d, e\}$
The star-partition algorithm first computes $\mathit{TH} = \left\{ (\texttt{c},\texttt{a}),(\texttt{c},\texttt{b}),(\texttt{e},\texttt{b}) \right\},$ as the edges from satellites to centers.
Now, it maps each $\texttt{T}$ vertex to its $\texttt{H}$, and merges these maps into a set (no duplicate keys): $P_s = \left\{ \texttt{c} \mapsto \texttt{b},\texttt{e} \mapsto \texttt{b} \right\}.$
Now for all remaining vertices $V_c = V \setminus \mathit{domain}(P) = \left\{ \texttt{a},\texttt{b},\texttt{d} \right\}$ we map them to themselves, giving: $P_c = \left\{ \texttt{a} \mapsto \texttt{a}, \texttt{b} \mapsto \texttt{b}, \texttt{d} \mapsto \texttt{d} \right\}.$ The vertices in $P_c$ are the centers.
Finally we merge $P_s$ and $P_c$ to obtain the partition map $P_s \cup P_c = \left\{ \texttt{a} \mapsto \texttt{a}, \texttt{b} \mapsto \texttt{b}, \texttt{c} \mapsto \texttt{b}, \texttt{d} \mapsto \texttt{d}, \texttt{e} \mapsto \texttt{b} \right\}.$
- $V'$ maps each vertex to itself
- to compute $TH$,
filterover edges $\Rightarrow O(\lg |E|) \in O(\lg |V|)$ - to compute $P$, use a nondeterministic inject to set each satellite $u$ to its center $v$, while eliminating duplicates. $\Rightarrow O(1)$
Star-partitioning has $O(|V| + |E|)$ work and $O(\lg |V|)$ span.
What is our contraction fraction?¶
$P_s$ determines the number of vertices removed at each iteration.
Since we want to ensure we are geoemtrically decreasing, we need to know how big $P_s$ will be in expectation.
Consider a vertex $v$ with neighbor $u$. For $v$ to be removed we must:
- flip a tails for $v$
- flip a heads for $u$
So, $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$ is the probability a vertex is removed.
$\Rightarrow \frac{1}{4} \cdot |V|$ vertices removed at each iteration, in expectation.
# We can now use star partitioning inside our contract_graph function.
def contract_graph(vertices, edges, partition_graph_f):
if len(edges) == 0:
return vertices, edges
else:
# partition the graph
# vertex_map is a dict from vertex->super_vertex
# e.g., {'a': 'a', 'b': 'a', 'c': 'a'...} in above example
new_vertices, vertex_map = partition_graph_f(vertices, edges)
# keep only cut eges
new_edges = set([(vertex_map(e[0]), vertex_map(e[1]))
for e in edges if vertex_map(e[0]) != vertex_map(e[1])])
return contract_graph(new_vertices, new_edges, partition_graph_f)
vertices = set(['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i'])
edges = set([('a', 'b'), ('a', 'c'), ('b', 'c'), ('b', 'g'),
('d', 'e'), ('d', 'f'), ('e', 'f'),
('h', 'i'), ('i', 'g'), ('h', 'g')])
contract_graph(vertices, edges, partition_graph_f)
Span of star contraction¶
Since we remove $\Rightarrow \frac{1}{4} \cdot |V|$ in expectation each iteration:
$$S(|V|) = S(3|V|/4) + \lg |V|$$Next time, we'll see a MST algorithm that uses contraction to have logarithmic span.