All pairs shortest path (APSP)¶
Up to now, we've consider the shortest paths from a fixed source node $s$.
We've solved the single source shortest paths problem with positive weights using Dijkstra's Algorithm.
$~~~$ Work $=O(|E|\log |V|)$
$~~~$ Span $=O(|E|\log |V|)$
And the single source shortest paths problem with negative weights using Bellman-Ford.
$~~~$ Work: $O(|V| \cdot |E|)$
$~~~$ Span: $O(|V| \lg |V|)$
Of course, what if we want to know the shortest path from all nodes in the graph?
How can we use algorithms we have seen to do this?
All pairs shortest paths using Bellman-Ford¶
Just run Bellman-Ford $|V|$ times, once per vertex.
Since one run of Bellman-Ford has $O(|V| \cdot |E|)$ work, the total work is $O(|V|^2 \cdot |E|)$
Can we do better?
Graph transformations¶
It would be great if we could instead just run Dijkstra's algorithm $|V|$ times, resulting in $O(|V|\cdot|E| \log |V|)~$ $<<~O(|V|^2 \cdot |E|)$
But, we can't run Dijkstra if the graph has negative edge weights.
Key idea: Let's find a transformation from $G=(V,E)$ to $G'=(V,E')$, where all the edges in $E'$ are non-negative.
We'll keep the nodes and edges the same, but just change the weights somehow...
This transformation must have the following two properties:
- shortest paths: The shortest path connecting $u$ to $v$ in $G$ should be the same in $G'$.
- non-negative edge weights: all edges in $G'$ should have weight $\ge 0$.
Naive transformation¶
What if we just find the smallest weight and add its absolute value to all weights?
Unfortunately, this won't work because it adds more weight to longer paths (in the sense of number of hops) than shorter ones.
For example:
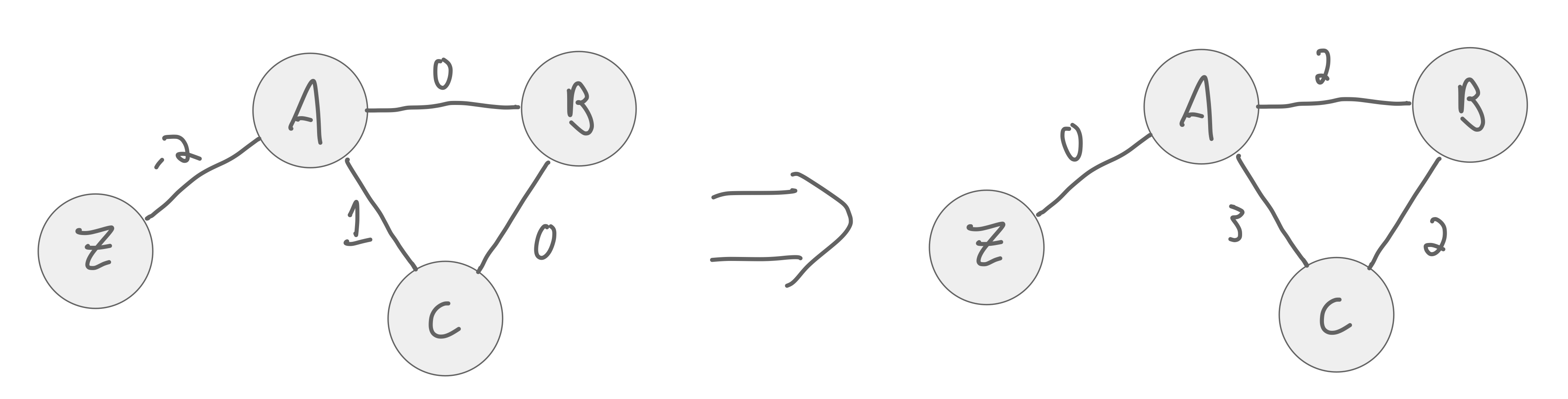
The shortest path $\delta_G(A,C)$ in origin graph is $A \rightarrow B \rightarrow C$.
It is $A \rightarrow C$ after the transformation
We haven't preserved shortest paths.
Preserving shortest paths¶
Consider some path from $v_0$ to $v_k$ in $G$:
$p=\langle v_0, v_1, \ldots v_k \rangle$
- Original Graph
- let $w(p)$ be the sum of the edge weights in $p$ in the original graph $G$
- let $\delta(v_0, v_k)$ be the weight of the shortest path from $v_0$ to $v_k$ in the original graph $G$
- Transformed Graph
- let $\hat{w}(p)$ be the sum of the edge weights in $p$ in the transformed graph $G'$
- let $\hat{\delta}(v_0, v_k)$ be the weight of the shortest path from $v_0$ to $v_k$ in the transformed graph $G'$
Then, we want a transformation such that: $w(p) = \delta(v_0, v_k) \leftrightarrow \hat{w}(p) = \hat{\delta}(v_0, v_k)$
- that is, $p$ is a shortest path from $v_0$ to $v_k$ with weights $w$ if and only if $p$ is also a shortest path with weights $w'$
Tranformation¶
let $f: V \mapsto \mathbb{R}$ be any function mapping vertices to real numbers.
claim: Weight transformations of the following form preserve shortest paths:
$$\hat{w}(u,v) = w(u,v) + f(u) - f(v)$$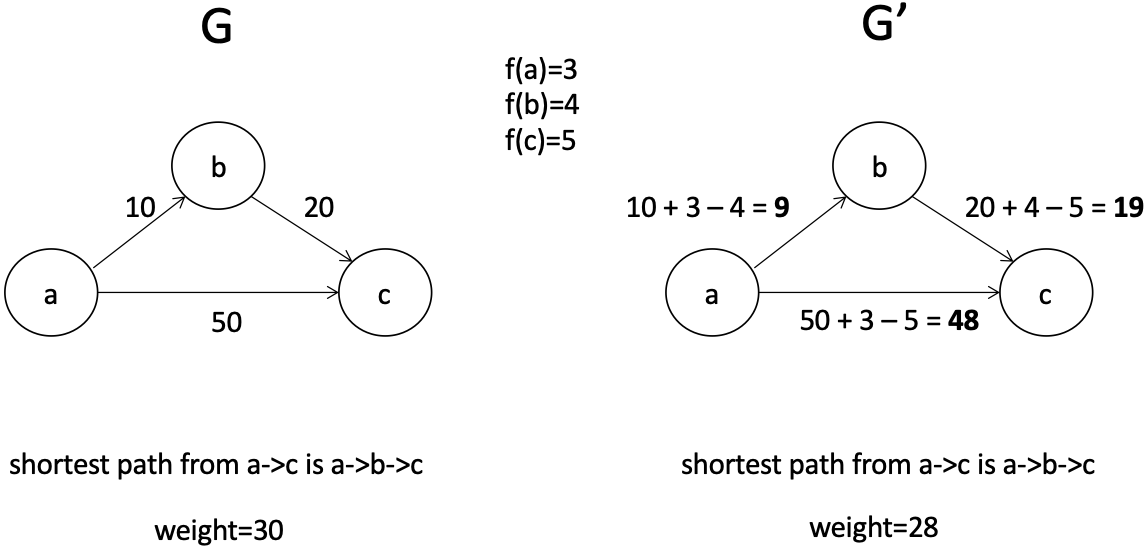
claim: Weight transformations of the following form preserve shortest paths:
$$\hat{w}(u,v) = w(u,v) + f(u) - f(v)$$proof:
First, show that $\hat{w}(p) = w(p) + f(v_0) - f(v_k)$
$ \begin{align} \hat{w}(p) & = \sum_{i=1}^k \hat{w}(v_{i-1}, v_i) & \hbox{by definition}\\ & = \sum_{i=1}^k \Big( w(v_{i-1}, v_i) + f(v_{i-1}) - f(v_i) \Big)& \hbox{by definition}\\ & = (w(v_0, v_1) + f(v_0) - \pmb{f(v_1))} + (w(v_1, v_2) + \pmb{f(v_1)} - \pmb{f(v_2)}) + \ldots + (w(v_{k-1}, v_k) + \pmb{f(v_{k-1})} - f(v_k))& \hbox{expanding}\\ & = w(p) + f(v_0) - f(v_k) & \hbox{cancelling terms} \end{align} $
Now show that if $\hat{w}(p_i) < \hat{w}(p_j)$, then $w(p_i) < w(p_j)$.
Consider comparing the weights of two paths $p_i$ and $p_j$ from $v_0$ to $v_k$.
$\hat{w}(p_i) = w(p_i) + f(v_0) - f(v_k)$
$\hat{w}(p_j) = w(p_j) + f(v_0) - f(v_k)$
Because the start and end nodes are the same, we can show that
$w(p_i) < w(p_j) \leftrightarrow \hat{w}(p_i) < \hat{w}(p_j)$
$ \begin{align} \hat{w}(p_i) &< \hat{w}(p_j)\\ w(p_i) + f(v_0) - f(v_k) &< w(p_j) + f(v_0) - f(v_k)\\ w(p_i) &< w(p_j) \end{align} $
Therefore, transformations of the form $\hat{w}(u,v) = w(u,v) + f(u) - f(v)$ preserve shortest paths $\blacksquare$.
Ensuring positive edge weights¶
Not all transformations $\hat{w}(u,v) = w(u,v) + f(u) - f(v)$ will result in positive edge weights.
We do know this about shortest paths:
triangle inequality:
$ \begin{align} \delta(s,v) & \le \delta(s,x) + w(x,v)\\ 0 & \le w(x,v) + \delta(s,x) - \delta(s,v) \end{align} $
which looks a lot like $w(u,v) + f(u) - f(v)$
So, if we can use shortest path as our function $f(v)$, we can ensure that weights are non-negative.
Ensuring positive edge weights¶
$\hat{w}(x,v) = w(x,v) + \delta(s,x) - \delta(s,v)$
But, what is the source of this shortest path?
We can't just pick a random node, as not all other nodes may be reachable from it.
Instead, we'll create a "dummy" source node, and connect it with 0 weight to all nodes. This ensures all nodes get a shortest path less than $\infty$.
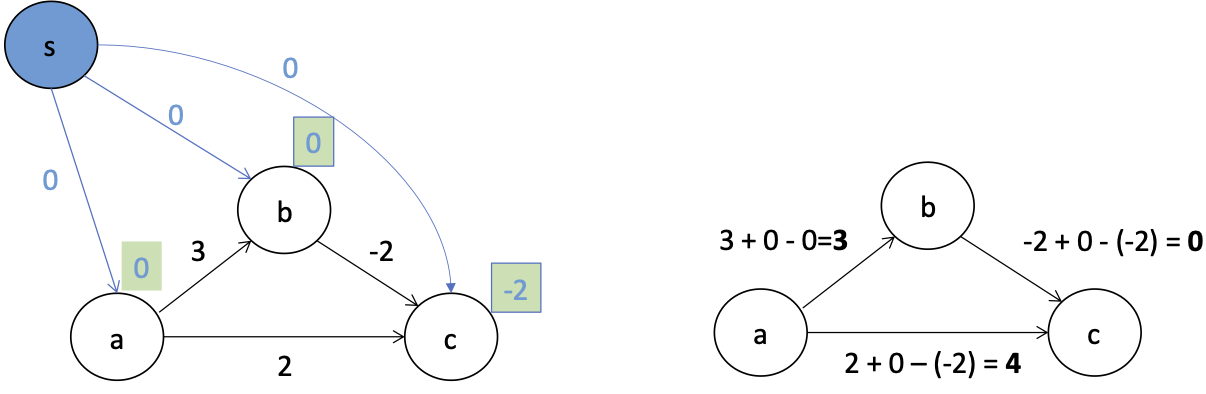
Putting it all together: Johnson's Algorithm¶
First, add source $s$ and edges from it to all other vertices with 0 cost:
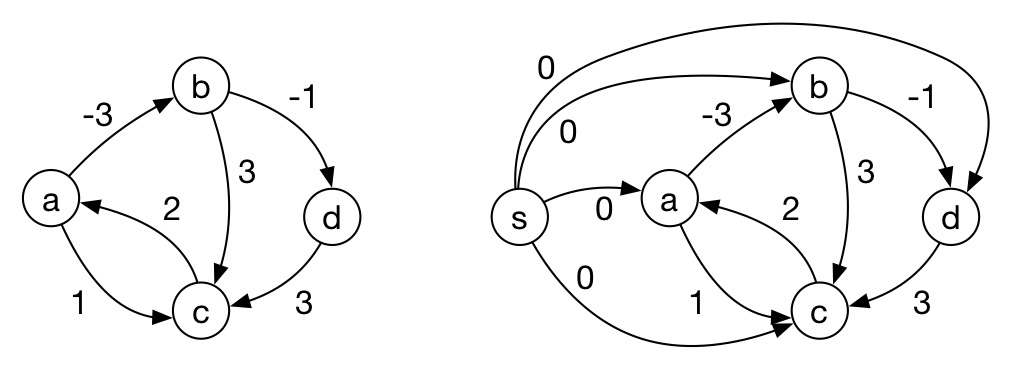
Next, run Bellman-Ford on this graph, resulting in distances $D[v]$, indicating the distance from $s$ to each $v$:
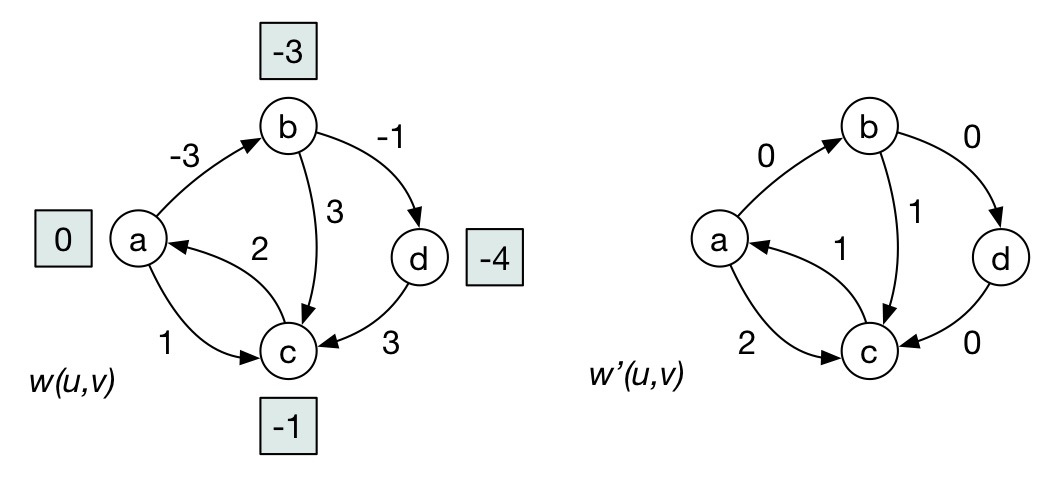
and update the graph using weights $w'(u,v) = w(u,v) + D[u] - D[v].~~~~$ E.g.
$$ \begin{align} w'(b,d) & = w(b,d) + D[b] - D[d]\\ & = -1 + (-3) - (-4) = 0 \end{align} $$We now have a final, modified graph: $G'$.
Finally, we can run Dijkstra's algorithm for each vertex in $G'$.
- we can do this in parallel
- We get $\delta_{G'}(u,v)$, the weight of the shortest path from $u$ to $v$ in $G'$, for all vertex pairs $(u,v) \in G$.
To compute $\delta_{G}(u,v)$, the shortest path distance in the original graph $G$:
$$ \delta_{G}(u,v) = \delta_{G'}(u,v) - D[u] + D[v]$$E.g, The shortest path from $a \rightarrow c$¶

def johnson(graph):
# add "dummy" node that links to all nodes with 0 cost.
for v, in_neighbors in graph.items():
in_neighbors.add(('s', 0))
graph['s'] = {}
# call bellmanford with new graph
distances = bellmanford(graph, 's')
print('bellman ford distances\n'+distances)
# create new graph with adjusted weights.
# b/c we'll be using Dijkstra, we'll use our original representation
# of a dict from node to set of out-neighbors.
new_graph = defaultdict(set)
for v, in_neighbors in graph.items():
for in_neighbor, weight in in_neighbors:
new_graph[in_neighbor].add((v, weight + distances[in_neighbor] - distances[v]))
print('\nnew graph')
pprint(dict(new_graph))
# now, run dijkstra on each node in the graph
print('\nunadjusted shortest paths')
apsp = {}
for v in new_graph:
if v != 's':
distances_from_v = dijkstra(new_graph, v)
# update final path scores
print(v, distances_from_v)
for u, dist in distances_from_v.items():
# adjust distances appropriately.
distances_from_v[u] = dist - distances[v] + distances[u]
apsp[v] = distances_from_v
print('\nadjusted shortest paths')
pprint(apsp)
return apsp
graph = {
'a': {('c', 2)},
'b': {('a', -3)},
'c': {('a', 1), ('b', 3), ('d', 3)},
'd': {('b', -1)},
}
result = johnson(graph)
bellman ford distances
{'a': 0, 'b': -3, 'c': -1, 'd': -4, 's': 0}
new graph
{'a': {('c', 2), ('b', 0)},
'b': {('c', 1), ('d', 0)},
'c': {('a', 1)},
'd': {('c', 0)},
's': {('d', 4), ('c', 1), ('b', 3), ('a', 0)}}
unadjusted shortest paths
c {'c': 0, 'a': 1, 'b': 1, 'd': 1}
a {'a': 0, 'b': 0, 'd': 0, 'c': 0}
d {'d': 0, 'c': 0, 'a': 1, 'b': 1}
b {'b': 0, 'd': 0, 'c': 0, 'a': 1}
adjusted shortest paths
{'a': {'a': 0, 'b': -3, 'c': -1, 'd': -4},
'b': {'a': 4, 'b': 0, 'c': 2, 'd': -1},
'c': {'a': 2, 'b': -1, 'c': 0, 'd': -2},
'd': {'a': 5, 'b': 2, 'c': 3, 'd': 0}}
Reduction¶
This is an example of a reduction! How?
We reduced the APSP problem with negative edge weights, to the APSP problem with positive edge weights.
- The cost of the reduction was $O(|V| \cdot |E|)$, the time to run Bellman-Ford
- The cost to solve the new version of the problem is $O(|V|\cdot|E| \log |V|)$
- Since the cost of the reduction is less than the transformed problem solution, this is an efficient reduction.
Cost of Johnson's Algorithm¶
- Add edges from $s$:
for v, in_neighbors in graph.items():
in_neighbors.add(('s', 0))
$~~~~~~~O(|V|)$
- Run Bellman-Ford
distances = bellmanford(graph, 's')
$~~~~~~~O(|V|\cdot |E|)$
- Adjust weights
$~~~~~~~~\hat{w}(x,v) = w(x,v) + \delta(s,x) - \delta(s,v)$
new_graph = defaultdict(set)
for v, in_neighbors in graph.items():
for in_neighbor, weight in in_neighbors:
new_graph[in_neighbor].add((v, weight + distances[in_neighbor] - distances[v]))
$~~~~~~~O(|E|)$
- Run Dijkstra $|V|$ times:
for v in new_graph:
if v != 's':
distances_from_v = dijkstra(new_graph, v)
$~~~~~~~O(|V|\cdot|E| \log |V|)$
- Adjust final path weights
for u, dist in distances_from_v.items():
distances_from_v[u] = dist - distances[v] + distances[u]
$~~~~~~~O(|E|)$
Finally tally¶
- Add edges from $s$
$~~~~O(|V|)$ - Run Bellman-Ford
$~~~~O(|V| \cdot |E|)$ - Adjust weights
$~~~~O(|E|)$ - Run Dijkstra $|V|$ times
$~~~~O(|V| \cdot |E| \log |V|)$ - Adjust final path weights
$~~~~O(|E|)$
Total work is then dominated by the cost of running Dijkstra's $|V|$ times:
$$\in O(|V|\cdot|E| \log |V|) $$