Agenda:
- depth-first search
- comparison with breadth-first search
- cycle detection
DFS | BFS |
 |
 |
While BFS uses a queue, we can implement DFS with a stack: last in first out
from collections import deque
def dfs_stack(graph, source):
def dfs_stack_helper(visited, frontier):
if len(frontier) == 0:
return visited
else:
node = frontier.pop()
print('visiting', node)
visited.add(node)
frontier.extend(filter(lambda n: n not in visited, graph[node]))
return dfs_stack_helper(visited, frontier)
frontier = deque()
frontier.append(source)
visited = set()
return dfs_stack_helper(visited, frontier)
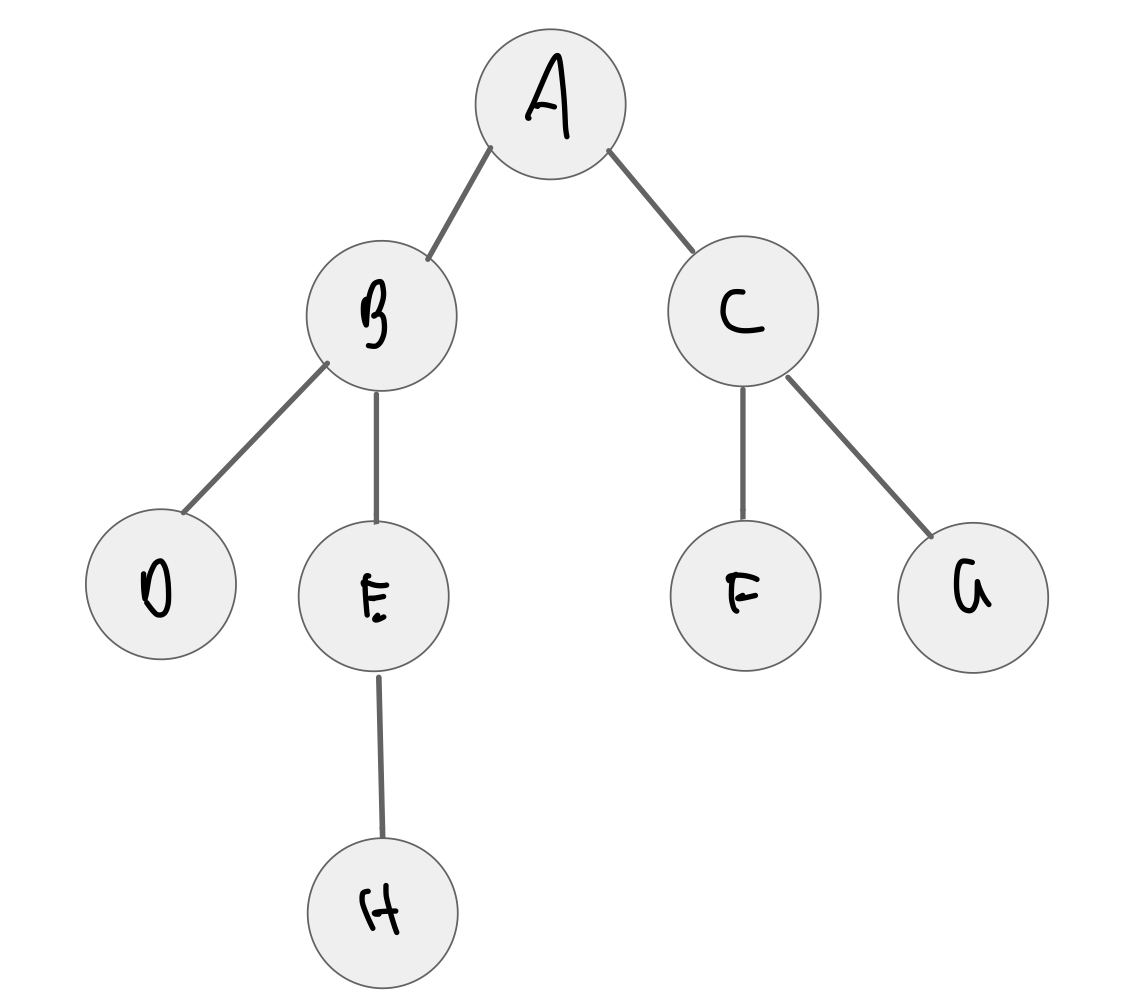
graph = {
'A': {'B', 'C'},
'B': {'A', 'D', 'E'},
'C': {'A', 'F', 'G'},
'D': {'B'},
'E': {'B', 'H'},
'F': {'C'},
'G': {'C'},
'H': {'E'}
}

dfs_stack(graph, 'A')
visiting A visiting B visiting D visiting E visiting H visiting C visiting F visiting G
{'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'}
Compare with bfs_serial!¶
def bfs_serial(graph, source):
def bfs_serial_helper(visited, frontier):
if len(frontier) == 0:
return visited
else:
node = frontier.popleft() # <==== DIFFERENCE
print('visiting', node)
visited.add(node)
frontier.extend(filter(lambda n: n not in visited, graph[node]))
return bfs_serial_helper(visited, frontier)
frontier = deque()
frontier.append(source)
visited = set()
return bfs_serial_helper(visited, frontier)
def dfs_stack(graph, source):
def dfs_stack_helper(visited, frontier):
if len(frontier) == 0:
return visited
else:
node = frontier.pop() # <======== DIFFERENCE
print('visiting', node)
visited.add(node)
frontier.extend(filter(lambda n: n not in visited, graph[node]))
return dfs_stack_helper(visited, frontier)
frontier = deque()
frontier.append(source)
visited = set()
return dfs_stack_helper(visited, frontier)
DFS with recursion¶
but wait, can't we just use recursion?
recursion maintains a stack of calls automatically.

def dfs_recursive(graph, source):
def dfs_recursive_helper(visited, node):
if node in visited:
return visited
else:
print('visiting', node)
visited.add(node)
iterate(dfs_recursive_helper, visited, list(graph[node]))
return visited
visited = set()
return dfs_recursive_helper(visited, source)
def iterate(f, x, a):
if len(a) == 0:
return x
else:
return iterate(f, f(x, a[0]), a[1:])

dfs_recursive(graph, 'A')
visiting A visiting C visiting G visiting F visiting B visiting E visiting H visiting D
{'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'}
Cost of DFS¶
As in DFS, we add a node to the visited set exactly once ($|V|$).
For each edge, we do one lookup to see if it exists in the visited set ($|E|$).
Thus, the total work is equivalent to BFS: $O(|V| + |E|)$.
Parallelism in DFS?¶
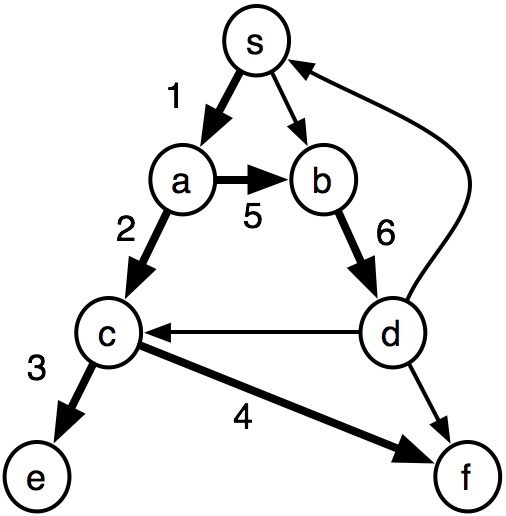
Is there any opportunity for parallelism?
One idea is to just run the search for each child in parallel.
- E.g., in this example, search subtree $a$ and $b$ in parallel
What potential problems arise?

- We may end up visiting $b$ twice (or $c$, or $f$)
- This isn't in DFS order! We shouldn't be visiting $b$ before $e$.
DFS belongs to a class of problems called P-complete: computations that most likely do not admit solutions with polylogarithmic span.
Cycle detection¶
How can we modify DFS to determine if the graph has a cycle?
cycle: a path in which all nodes are distinct except the first and last
- in an undirected graph, a cycle must contain at least three nodes
idea: determine whether a vertex is visited more than once.
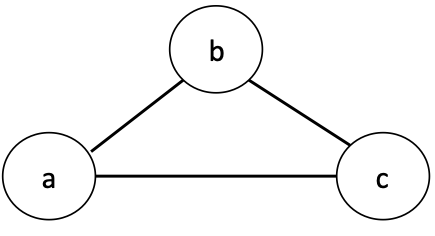

Determine whether a vertex is visited more than once but...the second visit must be from a different source
def dfs_stack_helper(visited, frontier):
if len(frontier) == 0:
return visited
else:
node = frontier.pop()
print('visiting', node)
visited.add(node)
frontier.extend(filter(lambda n: n not in visited, graph[node]))
return dfs_stack_helper(visited, frontier)
e.g., if $a$ is the source, we will see $b$ twice
- once when it is added to
visited - once in the base case of the recursive call (
if node in visited), withcas the parent

We will see $a$ three times:
- once when it is added to
visited - twice in the base case of the recursive call (
if node in visited)- with
bas the parent - with
cas the parent
- with
So, we need to keep track of the parent of each recursive call, and make sure not to make a recursive call back to the parent.
def dfs_cycle(graph, source):
visited = set()
def dfs_cycle_helper(result, node, parent):
"""
We pack (visited, has_cycle) variables into a single result variable,
so we can use iterate.
"""
visited, has_cycle = result
if node in visited:
print('found cycle from %s to %s' % (parent, node))
return (visited, True)
else:
print('visiting', node)
visited.add(node)
# ignore the parent!
neighbors = list(filter(lambda n: n != parent, graph[node]))
# curry the dfs_cycle_helper function to set the parent variable
# to be the node we are visiting now.
fn = lambda r, n: dfs_cycle_helper(r, n, node)
res = iterate(fn, (visited, has_cycle), neighbors)
return res
return dfs_cycle_helper((visited, False), source, source)

dfs_cycle(graph, 'A')
visiting A visiting C visiting G visiting F visiting B visiting E visiting H visiting D
({'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'}, False)
graph2 = {
'A': {'B', 'C'},
'B': {'A', 'D', 'E'},
'C': {'A', 'F', 'G'},
'D': {'B'},
'E': {'B', 'H'},
'F': {'C'},
'G': {'C', 'A'}, # add cycle back to A from G
'H': {'E'}
}
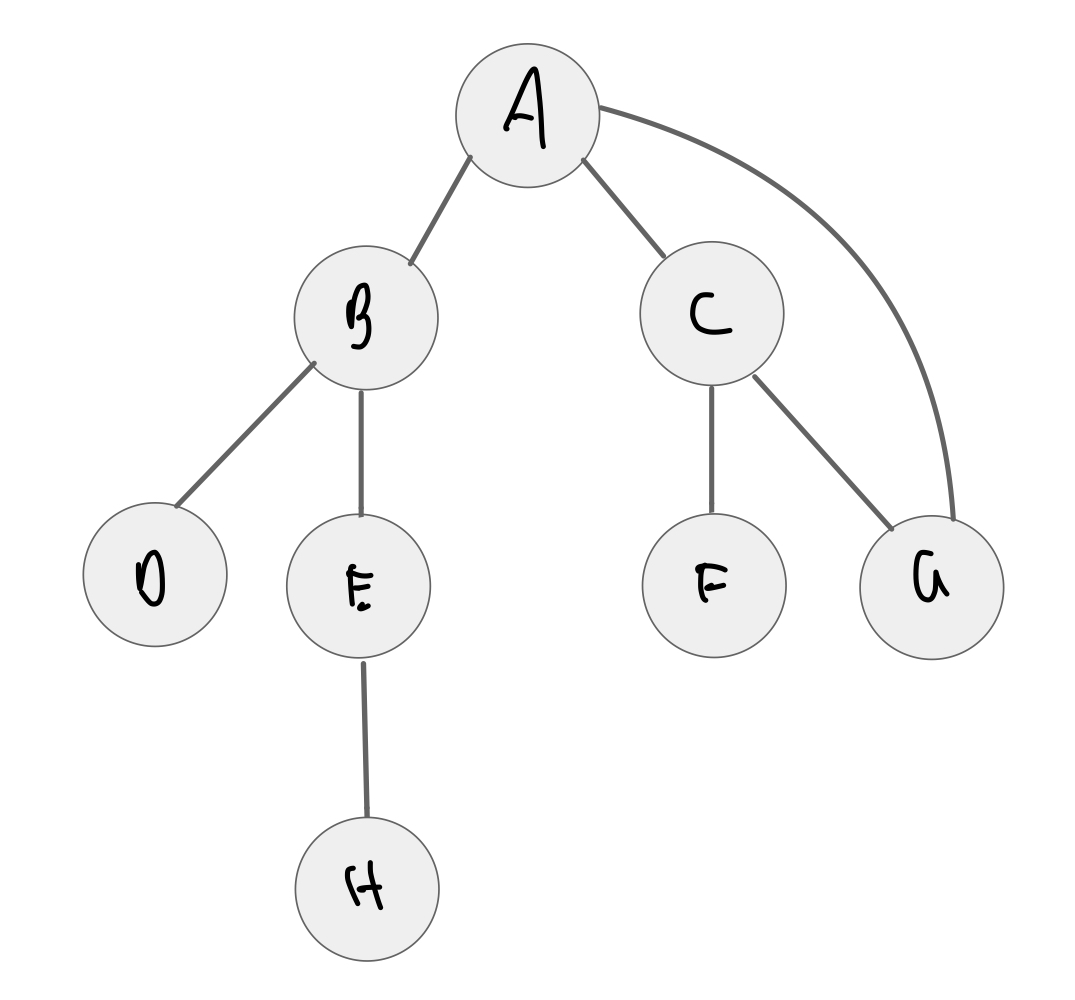

dfs_cycle(graph2, 'A')
visiting A visiting C visiting G found cycle from G to A visiting F visiting B visiting E visiting H visiting D
({'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'}, True)