CMPS 2200

Introduction to Algorithms

Breadth-first Search

Breadth-first search (BFS)

Input:

• graph $G$
• source vertex $s$

Process:

1. Visit neighbors of $s$
2. Visit neighbors of neighbors of $s$
3. Visit neighbors of neighbors of neighbors of $s$ ...

while ensuring that each node is visited only once.

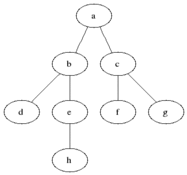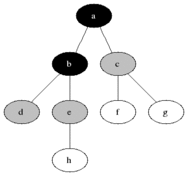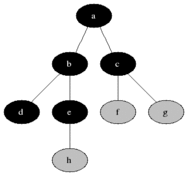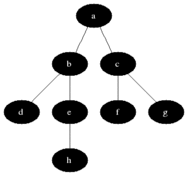
• Nodes at level $i$ have a path distance of $i$ from $s$
• BFS proceeds one level at a time, until there are no new neighbors to visit.

Building BFS

What variables will we need to keep track of?

• visited $X$: the nodes already visited, so we don't visit them more than once
• frontier $F$: the nodes to visit next.

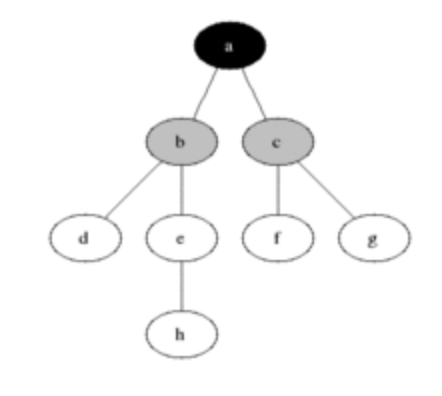
At iteration $i$:

• visited contains all nodes with distance less than $i$ from $s$
• frontier contains all nodes with distance exactly $i$ from $s$
  • these are all the unvisited neighbors of visited.

e.g., for $i=1$:

• $X_1 = \{a\}$
• $F_1 = \{b,c\}$

How do we update visited and frontier at each iteration?

• To update visited, we add any new values encountered in the frontier:
  • $X_{i+1} = X_i \cup F_i$

• To update frontier, we take the neighborhood of $F_i$ and remove any vertices that have already been visited:
  • $F_{i+1} = N(F_i) \setminus X_{i+1}$
  • $N(F_i)$ are the neighbors of the nodes in $F_i$

e.g. for $i=1$:

$X_1 = \{a\}$

$F_1 = \{b,c\}$

update:

• $X_2 = \{a\} \cup \{b,c\} = \{a,b,c\}$

• $F_2 = \{a, d, e, f, g\} \setminus \{a,b,c\} = \{d,e,f,g\}$

from functools import reduce

def bfs_recursive(graph, source):
    
    def bfs_helper(visited, frontier):
        if len(frontier) == 0:
            return visited
        else:
            # update visited
            # X_{i+1} = X_i OR F_i
            visited_new = visited | frontier
            print('visiting', (visited_new - visited))
            visited = visited_new

            # update frontier
            # F_{i+1} = N(F_i) \ X_{i+1}
            frontier_neighbors = reduce(set.union, [graph[f] for f in frontier])
            frontier = frontier_neighbors - visited
            return bfs_helper(visited, frontier)

    visited = set()
    frontier = set([source])        
    return bfs_helper(visited, frontier)

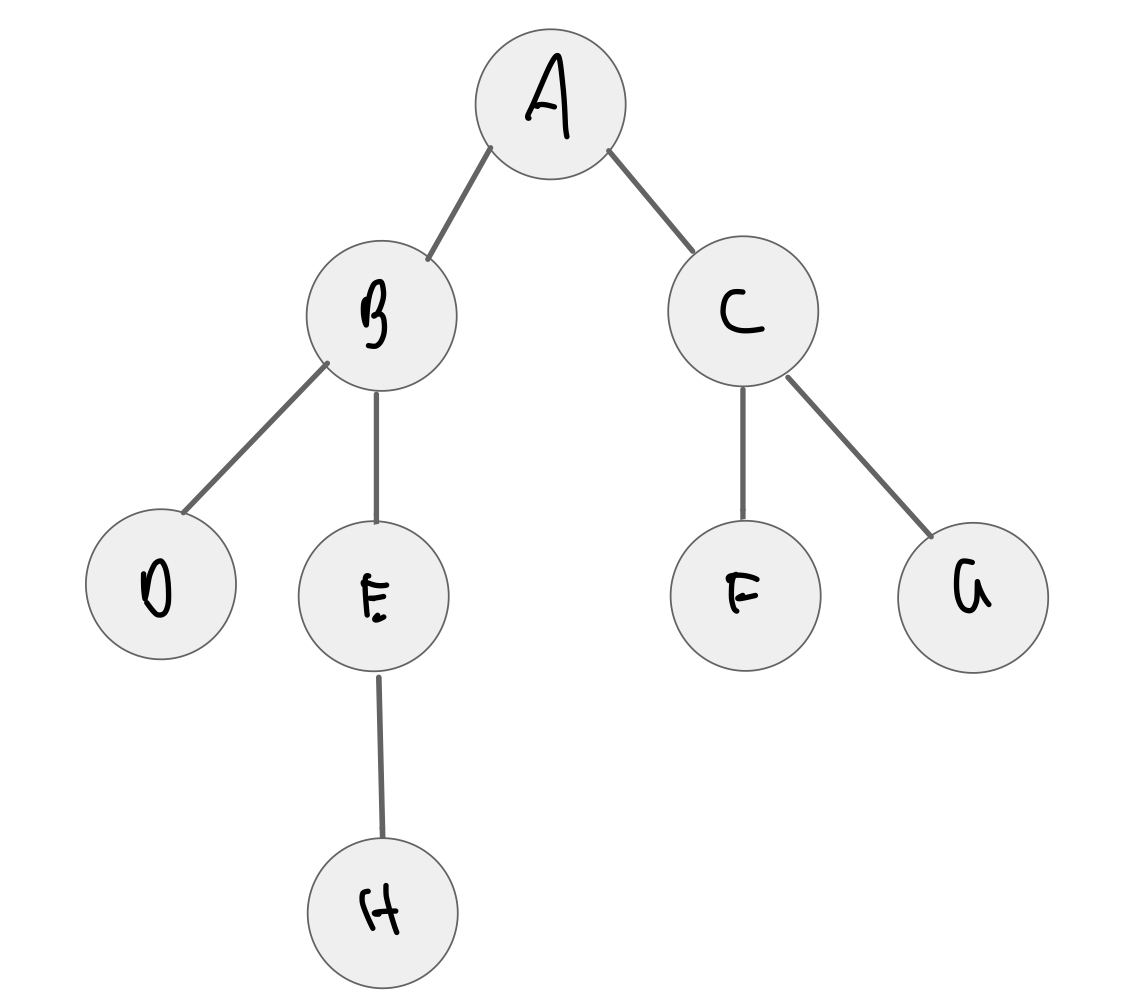
# same as example graph above
graph = {
            'A': {'B', 'C'},
            'B': {'A', 'D', 'E'},
            'C': {'A', 'F', 'G'},
            'D': {'B'},
            'E': {'B', 'H'},
            'F': {'C'},
            'G': {'C'},
            'H': {'E'}
        }

bfs_recursive(graph, 'A')

visiting {'A'}
visiting {'B', 'C'}
visiting {'G', 'E', 'D', 'F'}
visiting {'H'}

{'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'}

Work of BFS

• Since we have no recurrence, we will instead simply add up costs of each level.
• But, work done at each level varies depending on how many nodes it contains.

What we do know:

• Every reachable node appears in the frontier exactly once
• Likewise, each edge is processed exactly once

How much work is done for each node/edge?

• visited_new = visited | frontier
  • each node is added to the visited set at most once

• frontier_neighbors = reduce(set.union, [graph[f] for f in frontier])
  • each edge is added to frontier_neighbors at most twice (a->b, b->a)

• frontier = frontier_neighbors - visited
  • each node is removed from the frontier at most once.

• Therefore work is $O(|V| + |E|)$

Parallelism in BFS

There is some limited parallelism possible in BFS. While we must visit each level sequentially, at each level we can parallelize the set operations:

visited_new = visited | frontier

frontier_neighbors = reduce(set.union, [graph[f] for f in frontier])

frontier = frontier_neighbors - visited

We can represent a set as a binary search tree, which supports $O(\lg n)$ span operations for union, intersection, and difference operations. (See Vol II Ch 17 for more details).

• visited_new = visited | frontier
  • $O(\lg n)$ span

• frontier_neighbors = reduce(set.union, [graph[f] for f in frontier])
  • $O(\lg^2 n)$
    • reduce has $O(\lg n)$ span, but the union call at each step has $O(\lg n)$ span

• frontier = frontier_neighbors - visited
  • $O(\lg n)$ span

If the distance from the source to the most distant node is $d$, then the span is $O(d \lg^2 n)$

What shape graph results in the worst span?

Span $O(|V| \lg^2 n)$

Serial BFS

Alternatively: represent frontier with a queue, and remove one node at a time.

"first in first out"

• add newly discovered nodes to the end of the list
• at each iteration, remove the first node in the list

# deque is a double ended queue
# a doubly linked list 
from collections import deque
q = deque()
q.append(1)
q.append(2)
q.append(3)
print(q)
print('popleft returns: %d' %  q.popleft())
print(q)
print('pop returns: %d' %  q.pop())
print(q)

deque([1, 2, 3])
popleft returns: 1
deque([2, 3])
pop returns: 3
deque([2])

# compare with:
a = [1,2,3]
print(a)
print('pop returns', a.pop(0))

[1, 2, 3]
pop returns 1

What is running time to remove first element of a dynamic array with $n$ elements (a list in Python)?

$O(n)$: Need to shift all elements to the left.

What is the running time to remove first element of a doubly linked list $n$ elements (a deque in Python)?

$O(1)$

See more: https://wiki.python.org/moin/TimeComplexity

def bfs_serial(graph, source):
    def bfs_serial_helper(visited, frontier):
        if len(frontier) == 0:
            return visited
        else:
            node = frontier.popleft()
            print('visiting', node)
            visited.add(node)
    #         for n in graph[node]:
    #             if n not in visited:
    #                 frontier.append(n)
            # in parallel
            frontier.extend(filter(lambda n: n not in visited, graph[node]))
            return bfs_serial_helper(visited, frontier)

    frontier = deque()
    frontier.append(source)
    visited = set()
    return bfs_serial_helper(visited, frontier)

bfs_serial(graph, 'A')

visiting A
visiting C
visiting B
visiting F
visiting G
visiting D
visiting E
visiting H

{'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'}

Serial BFS Work/Span

Work and span are $O(|V| + |E|)$, since each vertex and edge are visited once.

How can we keep track of the distance each node is from the source?

def bfs_recursive_depths(graph, source):
    def bfs_helper_depths(visited, frontier, cur_depth, depths):
        if len(frontier) == 0:
            return depths
        else:
            # update visited
            # X_{i+1} = X_i OR F_i
            visited_new = visited | frontier
            print('visiting', (visited_new - visited))
            # record the depths of visited nodes
            for v in visited_new - visited:
                depths[v] = cur_depth
            visited = visited_new        
            # update frontier
            # F_{i+1} = N(F_i) \ X_{i+1}
            frontier_neighbors = reduce(set.union, [graph[f] for f in frontier])
            frontier = frontier_neighbors - visited
            return bfs_helper_depths(visited, frontier, cur_depth+1, depths)    

    depths = dict()
    visited = set()
    frontier = set([source])
    return bfs_helper_depths(visited, frontier, 0, depths)
     
bfs_recursive_depths(graph, 'A')

visiting {'A'}
visiting {'C', 'B'}
visiting {'G', 'F', 'D', 'E'}
visiting {'H'}

{'A': 0, 'C': 1, 'B': 1, 'G': 2, 'F': 2, 'D': 2, 'E': 2, 'H': 3}