CMPS 2200¶

Introduction to Algorithms¶

Introduction to Graphs¶

Agenda:

  • Overview of graphs

Terminology¶

A graph $G$ consists of

  • a set of $n$ vertices/nodes $V$
  • a set of $m$ edges $E \subseteq V \times V$

A graph is way to represent objects and their relations

  • Node: represents an object
  • Edge: represents a relation between two nodes.
  • Neighbor: Two nodes are neighbors if they are connected by an edge.
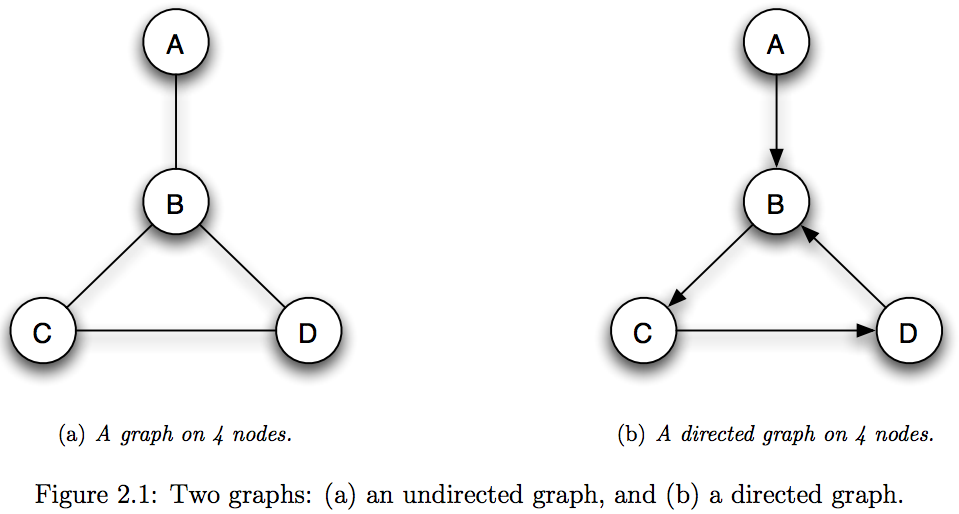
    • Directed Graph: Represents asymmetric (one-way) relationships
    • Undirected Graph: Represents symmetric relationships

Source

Graph examples¶

  • social networks (Twitter, Facebook, real-world)
  • web link graph
  • transportation
  • gas pipelines
  • disease spread

source

  • 6-degrees of Kevin Bacon

Source

Also interesting: Erdös-Bacon Number

Source

Graphs queries¶

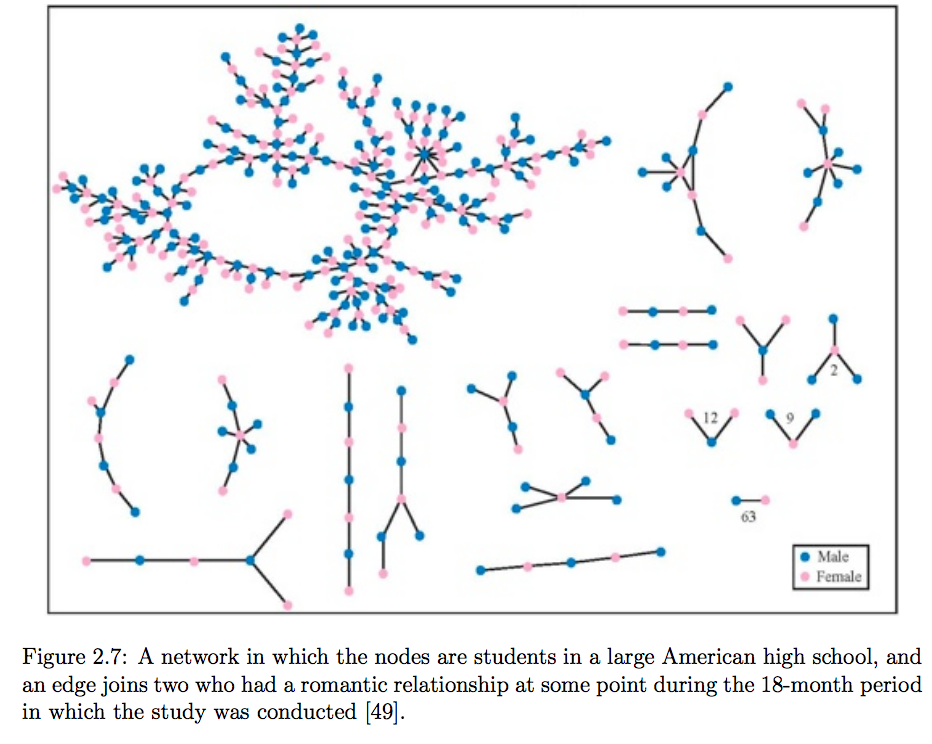
What are some things you might want to know about a graph? E.g., consider social networks, transport network, etc.

  • Who is friends with Billie Eilish?

    • find neighbors of a node:

      $ N(v) =\{v_i ~ \mid (v, v_i) \in E ~~ \hbox{or} ~~(v_i, v) \in E\}$

  • How popular is Billie Eilish?

    • degree: number of neighbors of a node:

      $ |N(v)|$

  • Do I know someone who is friends with Billie Eilish?
    • path: a sequence of nodes in which each consecutive pair are neighbors
    • reachability: $a$ is reachable from $b$ if there is a path between them
  • Am I in the same clique as Billie Eilish?
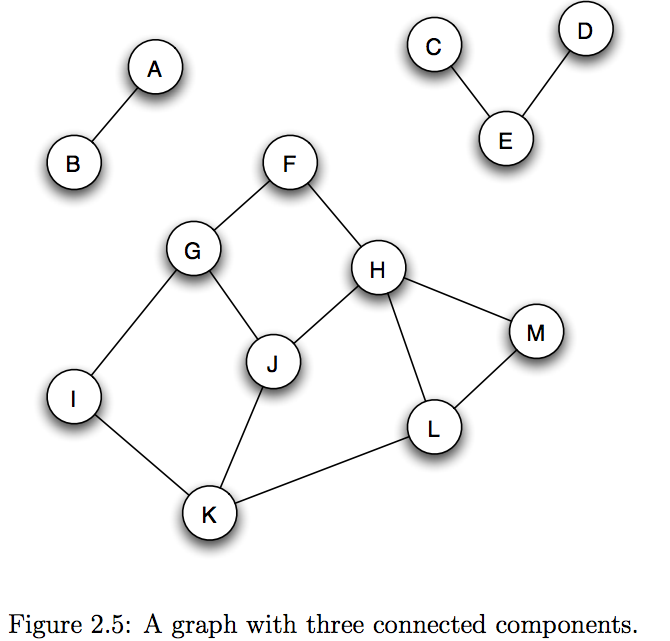
    • a graph is connected if there is a path between each pair of nodes
    • connected component: A maximal subset of nodes such that each pair of nodes is connected

Source

What data structures can we use to represent a graph?¶

Adjacency matrix¶

$ \begin{bmatrix} & A & B & C & D\\ A & 0 & 1 & 0 & 0\\ B & 1 & 0 & 1 & 1\\ C & 0 & 1 & 0 & 1\\ D & 0 & 1 & 1 & 0\\ \end{bmatrix} \begin{bmatrix} & A & B & C & D\\ A & 0 & 1 & 0 & 0\\ B & 0 & 0 & 1 & 0\\ C & 0 & 0 & 0 & 1\\ D & 0 & 1 & 0 & 0\\ \end{bmatrix} $

In [1]:
import numpy as np
from tabulate import tabulate
labels = ['A', 'B', 'C', 'D']
nodes = [0,1,2,3]
edges = [(0,1), (1,2), (2, 3), (3, 1)]

def make_graph(nodes, edges, directed=False):
    graph = np.zeros((len(nodes), len(nodes)), dtype=int)
    for e in edges:
        graph[e[0], e[1]] = 1
        if not directed: # add reverse direction
            graph[e[1], e[0]] = 1
    return graph
In [2]:
        
graph = make_graph(nodes, edges, directed=False)
print('undirected')
print(tabulate(graph, labels))
      

undirected
  A    B    C    D
---  ---  ---  ---
  0    1    0    0
  1    0    1    1
  0    1    0    1
  0    1    1    0
In [3]:
digraph = make_graph(nodes, edges, directed=True)
print('\ndirected')
print(tabulate(digraph, labels))

directed
  A    B    C    D
---  ---  ---  ---
  0    1    0    0
  0    0    1    0
  0    0    0    1
  0    1    0    0
In [21]:
def neighbors_adjacency(graph, node, labels):
    result = []
    i = labels.index(node)
    print(graph[i])
    for index, val in enumerate(graph[i]):
        if val == 1:
            result.append(labels[index])
    return result
    
neighbors_adjacency(graph, 'B', labels)

[1 0 1 1]
Out[21]:
['A', 'C', 'D']

Runtime to access neighbors of a node?

$O(|V|)$

Why is this space inefficient?¶

If there are $|V|$ nodes, what is the maximum number of edges?

$$\frac{|V|(|V|-1)}{2} \in O(|V|^2)$$

....but, if a graph is dense, then there's not really any value in representing the data as a graph.

Luckily, most real-world graphs are extremely sparse.

  • E.g., you are probably not friends with over 1,000 people.

it's a small world after all...¶

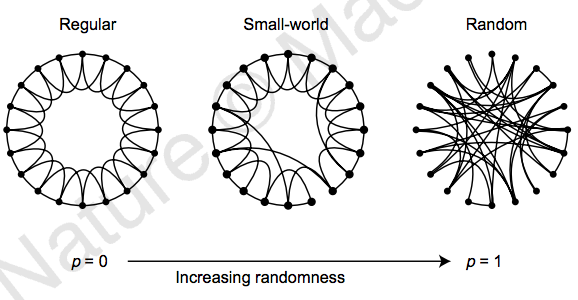
small

Source: Collective dynamics of 'small-world' networks. Duncan J. Watts & Steven H. Strogatz

Edge Sets¶

We could simply store the graph as a set of edges.

In [4]:
edges = set([('A', 'B'),
             ('B', 'C'),
             ('C', 'D'),
             ('D', 'B')])
edges
Out[4]:
{('A', 'B'), ('B', 'C'), ('C', 'D'), ('D', 'B')}

What's the space requirement?

$O(|E|)$

How can we access the neighbors of a node?

In [5]:
def neighbors_set(edges, node):    
    # assuming an undirected graph
    result = []
    for e in edges:
        if e[0] == node:
            result.append(e[1])
        elif e[1] == node:
            result.append(e[0])
    return result

neighbors_set(edges, 'B')
Out[5]:
['A', 'D', 'C']

What is the work/span of accessing neighbors using an edge set?

Work: $O(|E|)$

Span: $O(\lg |E|)$ (using filter)



Can we do better?

Map of Neighbors¶

We can use a hashmap (dict) to store the neighbors of each node.

In [22]:
graph = {
            'A': {'B'},
            'B': {'A', 'C', 'D'},
            'C': {'B', 'D'},
            'D': {'B', 'C'}
        }
graph
Out[22]:
{'A': {'B'}, 'B': {'A', 'C', 'D'}, 'C': {'B', 'D'}, 'D': {'B', 'C'}}

What is work of accessing neighbors?

In [7]:
def neighbors_map(graph, node):
    return graph[node]

neighbors_map(graph, 'B')
Out[7]:
{'A', 'B', 'D'}

Constant time to lookup the neighbors of a node.

Graph Search¶

One of the fundamental operations over graphs

  • Start at a source node s
  • Visit all reachable nodes
    • $t$ is reachable from $s$ if there is a path between them
  • For efficiency, visit each node at most once.



Can be used to solve a number of problem:

  • Is the graph connected?
  • Is node $t$ reachable from node $s$
  • Shortest path from $s$ to $t$

Generic Graph Search¶

Consider the task of crawling every web page reachable from a starting page $s$.

How would you do this?

At any point in the search, a vertex can be in one of three sets:

  • visited: the set of vertices already visited
  • frontier: the unvisited neighbors of the visited vertices
  • unseen: everything else

We can then describe a generic search algorithm as follows:

while vertices remain to be visited:

  • visit some unvisited nodes in the frontier
  • update the three sets


We'll look at two common search algorithms, breadth-first search and depth-first search.

Vertex Hopping¶

Just to get an idea of the problem, we'll start with an inefficient way of searching called vertex hopping

until all nodes visited:
    pick a node
    visit all its neighbors
In [23]:
def hop(graph):
    for v in graph:
        print('searching with %s' % v)
        for neighbor in graph[v]:
            print('...found %s' % neighbor)
            
hop(graph)

searching with A
...found B
searching with B
...found A
...found C
...found D
searching with C
...found B
...found D
searching with D
...found B
...found C

This of course ignores the idea of paths in a graph.

However, we could still build on this to solve the reachability problem. How? We'll address this problem in recitation.