Agenda:
- Longest Increasing Subsequence
- Edit Distance
Longest Increasing Subsequence¶
We've seen a few sequence algorithms:
- longest run
- maximum contiguous subsequence
- longest gap.
Let's look another trend we might want to identify from a sequence.
Given a sequence $S = \langle s_0, s_1, \ldots, s_{n-1} \rangle$, what is the longest increasing subsequence?
Note that subsequences don't need to be contiguous.
Example: $S=\langle 5, 2, 8, 6, 3, 6, 9, 7\rangle$.
Every subsequence of length 1 is trivially increasing.
Increasing subsequences include:
$\langle 2, 6, 9 \rangle$
$\langle 2, 8, 9 \rangle$
$\langle 5, 6, 7\rangle$
What is the longest?
$\langle 2, 3, 6, 9 \rangle$
$\langle 2, 3, 6, 7 \rangle$
Solving LIS¶
$$S=\langle 5, 2, 8, 6, 3, 6, 9, 7\rangle$$Let's reduce this problem to something slightly simpler with the observation that the longest increasing subsequence must start somewhere in $S$.
Let $\mathit{LIS}(S, i)$ be the longest increasing subsequence for $S$ that starts with $S[i]$ as the first element.
How can we use the function $\mathit{LIS}(S, i)$ to solve the original problem?
If we can compute $LIS(S, i)$ then we can compute $ \mathit{LIS}(S) = \max_{0\leq i < n} \mathit{LIS}(S, i).$
- If $S[i]$ is the first element, then the next element $j$ in the longest increasing subsequence must have $j>i$ and $S[j] > S[i]$.
- Whichever element is next, we must have $\mathit{LIS}(S, i) = 1 + \max_{j: S[j] > S[i]} \mathit{LIS}(S[j:]).$
Optimal Substructure¶
Optimal Substructure for Longest Increasing Subsequence: Given a sequence $S$, we have that the longest increasing subesquence of $S$ is $ \mathit{LIS}(S) = \max_{0\leq i < n} \mathit{LIS}(S, i)$ where $$\mathit{LIS}(S, i) = 1 + \max_{j: S[j] > S[i]} \mathit{LIS}(S, j).$$
To compute this optimal substructure property, how many distinct subproblems must be computed from scratch?
There are only a linear number of starting points for an optimal solution.
But for each subproblem, the work to compute an optimal solution, even if we have computed all subproblems already, is actually linear in the size of the sequence we consider.
This optimal substructure property is little different than what we saw in Knapsack where every subproblem depended on two subproblems which could be solved in $O(1)$ time.
Implementation: Top-down w/out memoization¶
# longest increasing subsequence starting at position 0
def LIS_helper(S):
if (S == []):
return(0)
else:
# find elements in the sequence that are larger than S[0]
rest = [j for j in range(1,len(S)) if S[j]>S[0]]
if (rest == []):
return(1)
else:
results = [LIS_helper(S[i:]) for i in rest]
if (results == []):
return(1)
else:
return(1 + max(results))
def LIS(S):
return(max([LIS_helper(L[i:]) for i in range(len(L))]))
L = [5,2,8,6,3,6,9,7]
print(LIS(L))
4
Runtime¶
For a list $S$ of length $n$, we incur $O(n^2)$ work if we reuse the results from already visited subproblems.
Since we decrease the length of the list by at least one element in each recursive call, the longest path in the DAG is $n$.
At each node, we require $O(\lg n)$ span to compute the max (e.g., using reduce), and $O(1)$ span to compute rest (using filter), so the span is $O(n \lg n).$
$W(n) \in O(n^2)$
$S(n) \in O(n \lg n)$
Edit Distance¶
Given two strings $S, T \in \Sigma^*$, how similar are they?
We can measure this using edit distance, which is the number of insertions and deletions needed to turn $S$ into $T$. Note that we can also go from $T$ to $S$ if we just reverse the edits (by turning insertions into deletions)
Example:
$S$ = abcdefghijkl
$T$ = abcdghikjl
How many edits are needed?
This might seem like a toy problem, but it is a critical problem in comparing gene and protein sequences. By attaching weights to insertions and deletions, we can assess the evolutionary distance between two sequences.
Notation Note:
We will represent insertions and deletions using dashes. All insertions and deletions refer to modifying the top string.
A dash in the bottom string means delete the character above it.
E.g.,
abc
a-c
A dash in the top string means insert a character here to match the character below.
E.g.,
jkl-l
jklol
Consider following edit sequence:
$S$: abcdefghijkl---
$T$: abcd--ghi---kjl
This has 5 deletions and 3 insertions, for a total of 8 edits.
What about this one:
$S$: abcdefghijk-l
$T$: abcd--ghi-kjl
We have 3 deletions and 1 insertion for a total of 4 edits.
Our goal is to compute the minimum edit distance between two strings $S$ and $T$ of lengths $m$ and $n$, respectively.
Greedy Solution?¶
Suppose we had the following two strings
$S=$relevant
$T=$elephant
and suppose we had a greedy choice:
If the characters match, do nothing, else insert into $S$:
$S=$--------relevant
$T=$elephant
Clearly not ideal, need to follow it up to delete all extra characters in $S$ past the end of $T$.
Runtime: S+T, literally the worst!
Greedy choice 2:
If the characters match, do nothing, else delete from $S$:
$S=$relevant
$T=$-ele----phant
Also not ideal.
Why isn't greedy working?¶
The choice we make at any particular position should depend on how it effects the rest of the problem.
We should examine both options, delete and insert, to decide what to do with respect to how that choice affects everything after.
Here is an optimal set of edits for "relevant elephant"
$S=$relev--ant
$T=$-ele-phant
Optimal substructure?¶
Let's use case-based reasoning about the optimal solution as we did for Knapsack.
Let $\mathit{MED}(S, T)$ be the optimal number of edits between $S$ and $T$.
In an optimal sequence of edits, how would we deal with the first two characters of $S$ and $T$, respectively?
Three cases:
$~~$ 1) $~~S$ or $T$ is empty
$~~$ 2) $~~S[0]=T[0]$
$~~$ 3) $~~S[0] \neq T[0]$
If either string is empty, then the edit cost is simply the length of the other string.
There is no benefit to editing position $0$. The edit distance is the edit distance of the tails of these strings.
$\mathit{MED}(S, T) = \mathit{MED}(S[1:], T[1:])$
e.g,
$\mathit{MED}(S, T) = \mathit{MED}($'bc'$, $'de'$)$.
3) $S[0] \neq T[0]$¶
S='abc'
T='bde'
We must either perform a deletion or insertion, whichever is less costly
Deleting from $S$. The cost is 1 (the cost of the deletion) plus the $\mathit{MED}$ of the tail of $S$ with all of $T$.
S='abc'
T='-bde'
$\mathit{MED}(S, T) = 1+\mathit{MED}($'bc','bde'$)$
$\mathit{MED}(S, T) = 1+\mathit{MED}(S[1:], T)$
Inserting into $S$. If we insert into $S$, we have to match up all of $S$, which still remains, with the tail of T since we've ensured its first character matches.
S='-abc'
T='bde'
$\mathit{MED}(S, T) = 1+\mathit{MED}($'abc','de'$)$
$\mathit{MED}(S, T) = 1+\mathit{MED}(S, T[1:])$
Optimal Substructure¶
Optimal Substructure for Edit Distance: Let $S$ and $T$ be strings of length $m$ and $n$. Then,
$$ \mathit{MED}(S, T) = \begin{cases} \mathit{MED}(S[1:], T[1:]), ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\texttt{if}~~S[0]=T[0] \\ 1+\min\{\mathit{MED}(S[1:], T),\mathit{MED}(S, T[1:])\}, ~~~~~\texttt{otherwise} \\ \end{cases} $$Problem Size¶
Just as with Knapsack, this recursion tree for this recurrence yields an exponential number of nodes. How many nodes are there, and what is the depth?
The recursion tree has $O(2^{m+n})$ nodes and depth $O(m+n)$. Are there shared subproblems?
For $S$=ABC and $T$=DBC we have the following DAG:
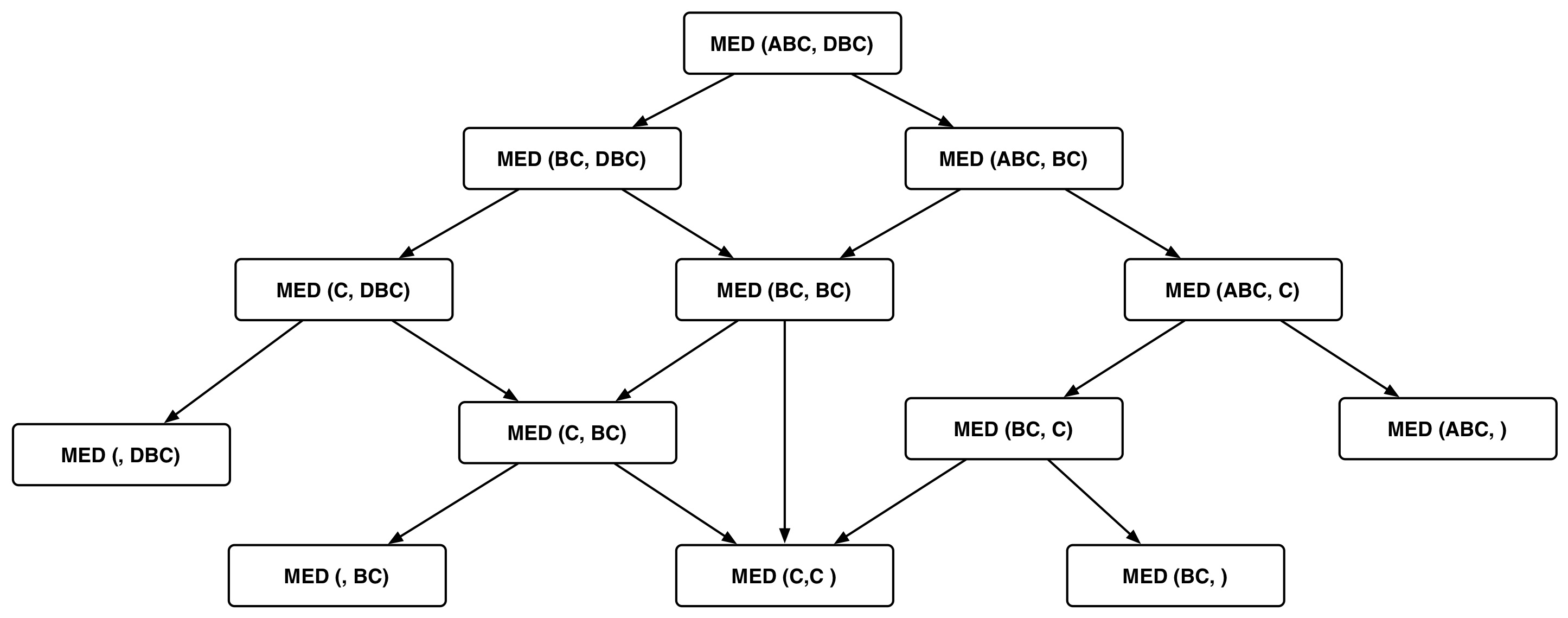
How much sharing is possible? In other words, how many distinct subproblems are there?

In any recursive call, the subproblems we consider consist of strings with one less character. So there are $O(mn)$ subproblems, each of which can each be computed in $O(1)$ time (if we have precomputed the necessary dependencies). The longest path in the recursion DAG is $O(m+n)$.
Implementation: Top-down w/out memoization¶
def MED(S, T):
#print("S:%s, T:%s" % (S, T))
if (S == ""):
return(len(T))
elif (T == ""):
return(len(S))
else:
if (S[0] == T[0]):
return(MED(S[1:], T[1:]))
else:
return(1 + min(MED(S, T[1:]), MED(S[1:], T)))
S= 'abcdefghijkl'
T= 'abcdghikjl'
# abcdefghijk-l
# abcd--ghi-kjl
print(MED(S, T))
4
S = 'relevant'
T = 'elephant'
# relev--ant
# -ele-phant
print(MED(S, T))
4
Solving MED using a Bottom-Up Approach¶
As we did for knapsack, we can use a table to calculate and store solutions to subproblems.
| Cost to Delete | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cost to Insert | '' | k | i | t | t | e | n | |
| '' | ||||||||
| s | ||||||||
| i | ||||||||
| t | ||||||||
| t | ||||||||
| i | ||||||||
| n | ||||||||
| g | ||||||||
We fill in the values in the first row to give the cost of deleting characters from 'kitten' to match the empty string '' to the left.
| Cost to Delete | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cost to Insert | '' | k | i | t | t | e | n | |
| '' | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| s | ||||||||
| i | ||||||||
| t | ||||||||
| t | ||||||||
| i | ||||||||
| n | ||||||||
| g | ||||||||
We fill in the values in the first column to give the cost of inserting characters from 'sitting' to match the empty string above.
| Cost to Delete | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cost to Insert | '' | k | i | t | t | e | n | |
| '' | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| s | 1 | |||||||
| i | 2 | |||||||
| t | 3 | |||||||
| t | 4 | |||||||
| i | 5 | |||||||
| n | 6 | |||||||
| g | 7 | |||||||
We fill in the rest using our recurrence:
$$ \mathit{MED}(S, T) = \begin{cases} \mathit{MED}(S[1:], T[1:]), ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\texttt{if}~~S[0]=T[0] \\ 1+\min\{\mathit{MED}(S[1:], T),\mathit{MED}(S, T[1:])\}, ~~~~~\texttt{otherwise} \\ \end{cases} $$| Cost to Delete | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cost to Insert | '' | k | i | t | t | e | n | |
| '' | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| s | 1 | 2 | ||||||
| i | 2 | |||||||
| t | 3 | |||||||
| t | 4 | |||||||
| i | 5 | |||||||
| n | 6 | |||||||
| g | 7 | |||||||
| Cost to Delete | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cost to Insert | '' | k | i | t | t | e | n | |
| '' | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| i | 2 | 3 | 2 | |||||
| t | 3 | |||||||
| t | 4 | |||||||
| i | 5 | |||||||
| n | 6 | |||||||
| g | 7 | |||||||
| Cost to Delete | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cost to Insert | '' | k | i | t | t | e | n | |
| '' | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| i | 2 | 3 | 2 | 3 | ||||
| t | 3 | |||||||
| t | 4 | |||||||
| i | 5 | |||||||
| n | 6 | |||||||
| g | 7 | |||||||
| Cost to Delete | ||||||||
|---|---|---|---|---|---|---|---|---|
| Cost to Insert | '' | k | i | t | t | e | n | |
| '' | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
| s | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| i | 2 | 3 | 2 | 3 | 4 | 5 | 6 | |
| t | 3 | 4 | 3 | 2 | 3 | 4 | 5 | |
| t | 4 | 5 | 4 | 3 | 2 | 3 | 4 | |
| i | 5 | 6 | 5 | 4 | 3 | 4 | 5 | |
| n | 6 | 7 | 6 | 5 | 4 | 5 | 4 | |
| g | 7 | 8 | 7 | 6 | 5 | 6 | 5 | |
Tracing back the edits¶
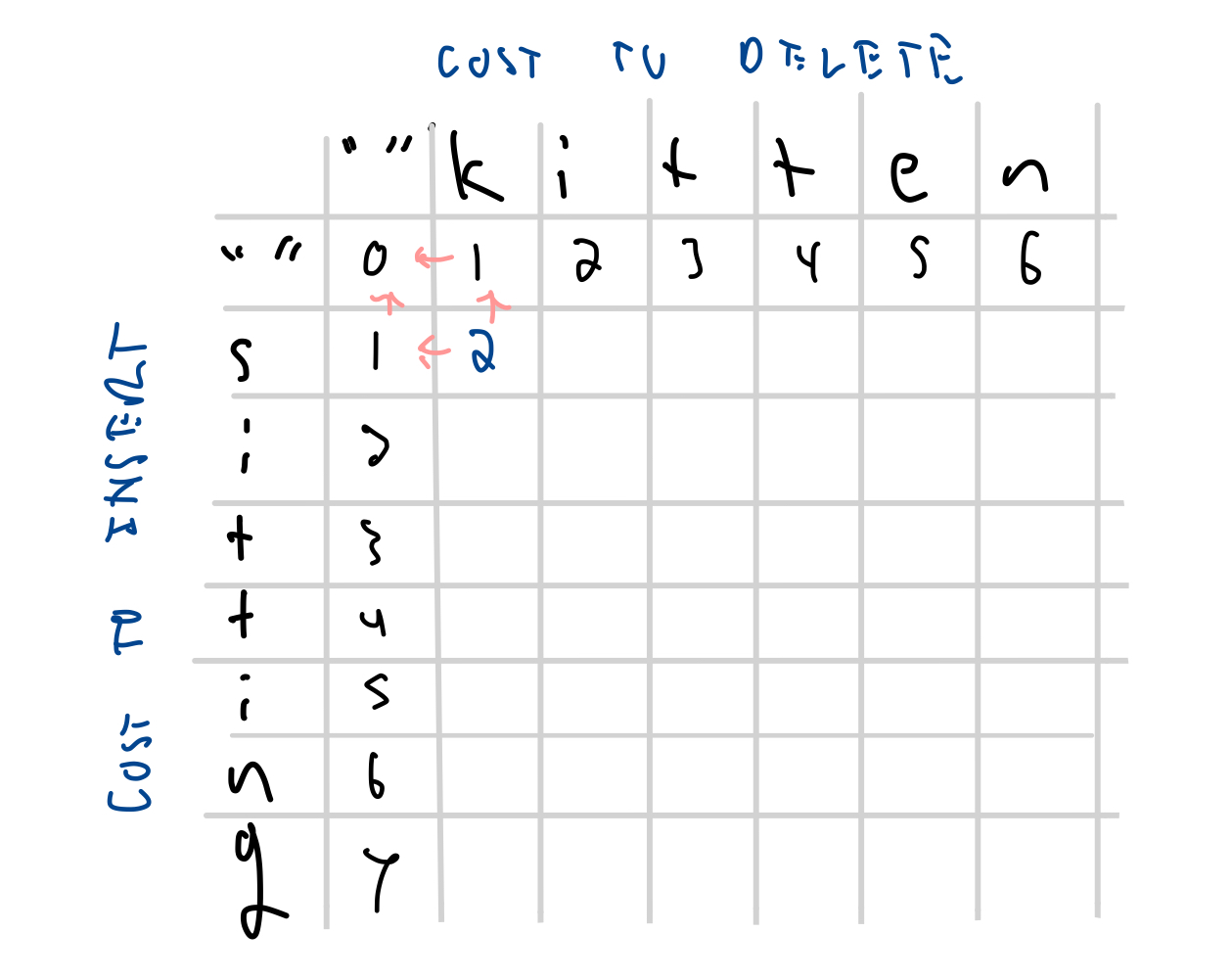
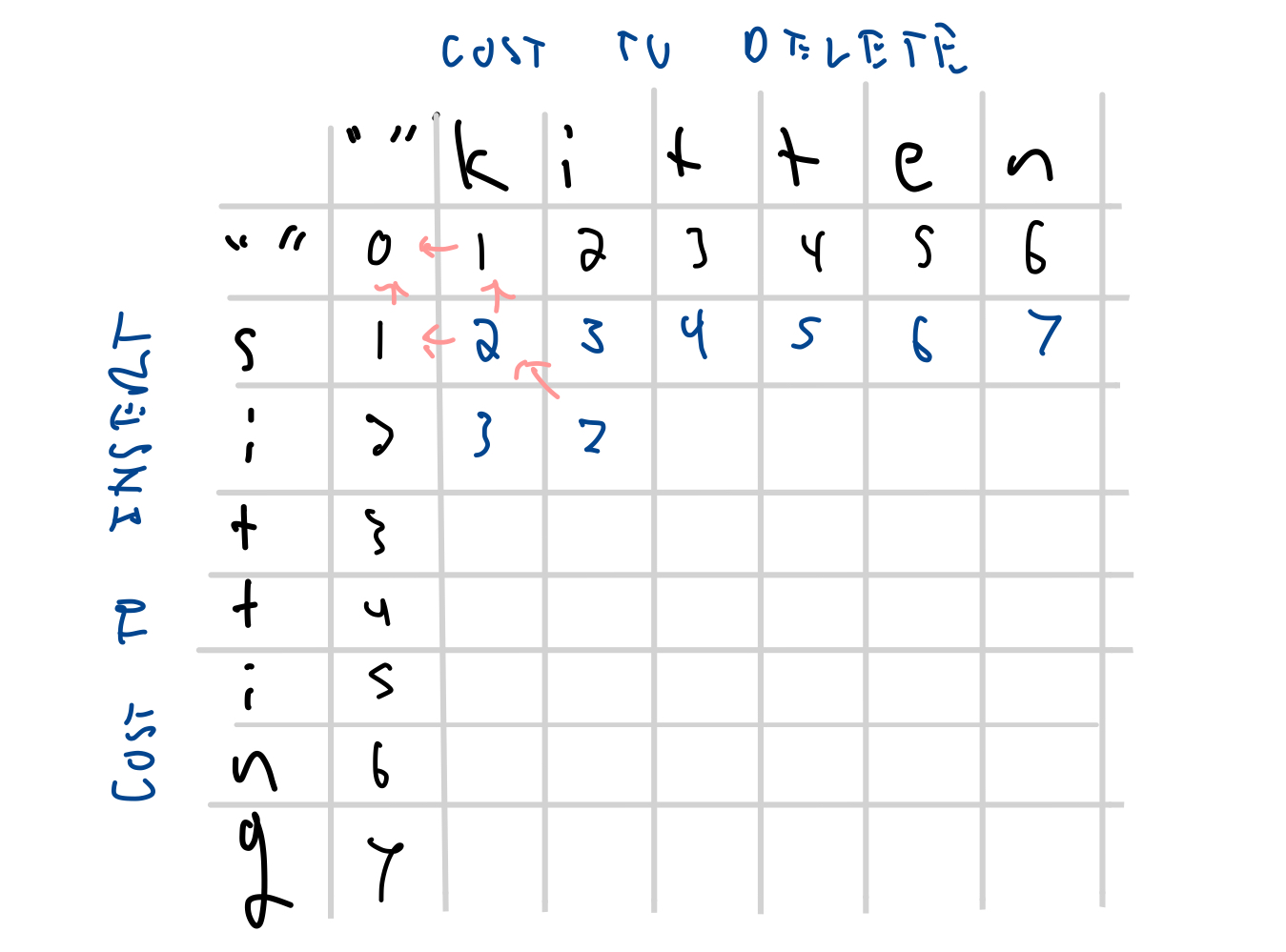
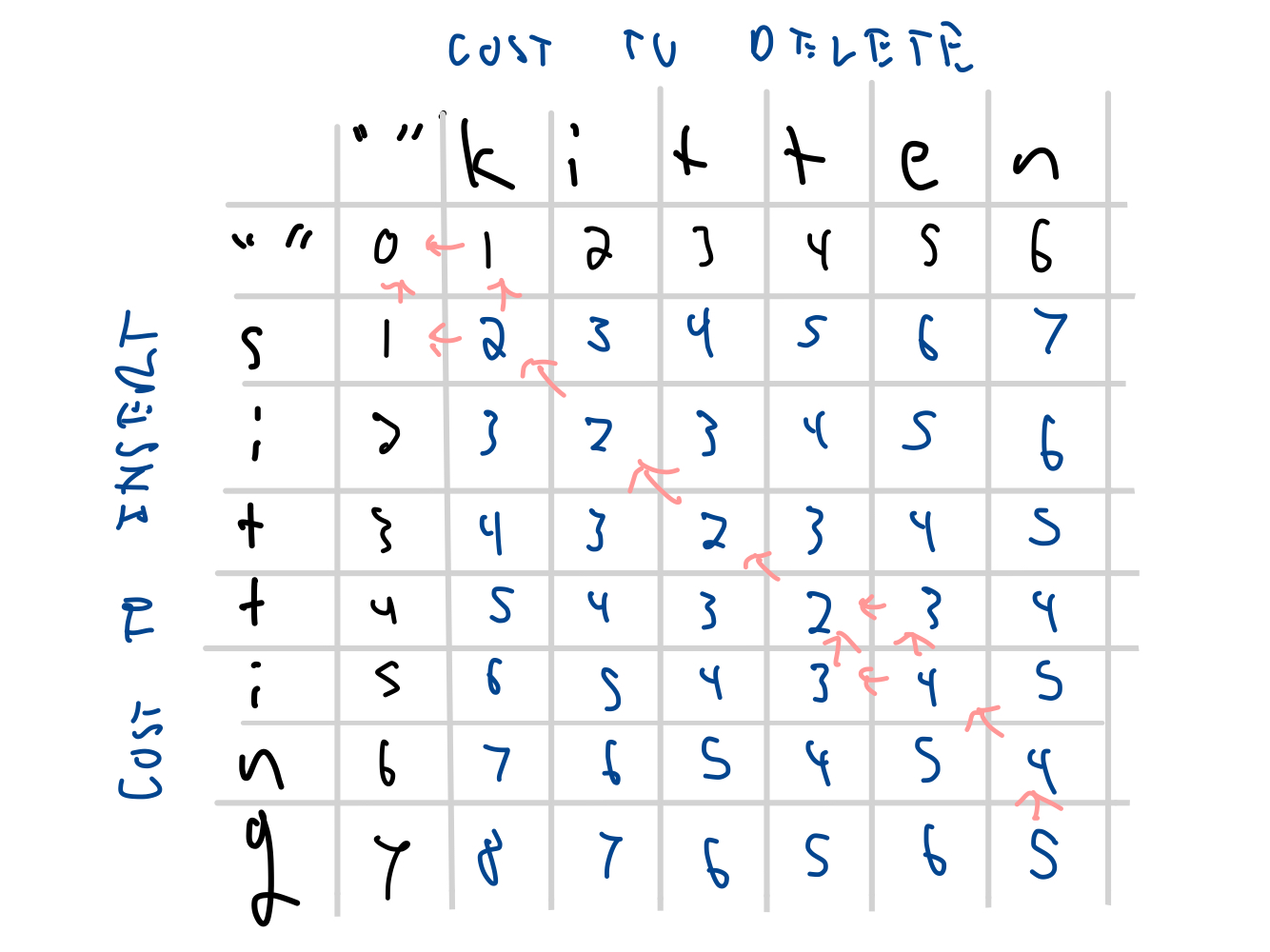
Alignments:
k-itte-n- $~~~~~~~$ -kitt-en-
-sitt-ing $~~~~~~~$ s-itti-ng
S = 'kitten'
T = 'sitting'
# -kitt-en-
# s-itti-ng
print(MED(S, T))
5