CMPS 2200¶

Introduction to Algorithms¶

Data Compression¶

Agenda:

Huffman Coding

Document encoding¶

If we are given a document $D$ in which we use the alphabet $\Sigma = \{\sigma_1 \ldots \sigma_k\}$, our goal is to create a binary encoding of $\Sigma$ to represent $D$ with as few bits as possible.

Of course, the encoding must distinctly represent $\Sigma$.

Example:

Suppose $\Sigma=\{A, B, C, D\}$, and document $D = \langle A, A, A, A, A, A, A, A, A, B, C, D\rangle$.

A naive encoding could be:

$$\sigma$$	$$e(\sigma)$$
A	00
B	01
C	10
D	11

This is a fixed-length encoding of $\Sigma$.

What is the number of bits required to encode the entire document with this encoding?

The length of the document with this encoding is $2\cdot 12 = 24$. The encoding is:

$e(D) = \texttt{"}000000000000000000011011\texttt{"}$

A more space-efficent encoding?¶

Fixed-length encoding doesn't account for redundancy in the document.

Intuitively, we should encode the document by the frequency of the characters in the alphabet. The more frequent the character, the smaller its code should be.

$D = \langle A, A, A, A, A, A, A, A, A, B, C, D\rangle$

$$\sigma$$	$$f(\sigma)$$
A	9
B	1
C	1
D	1

Let $f: \sigma \rightarrow \mathbb{Z}$ be the number of times a character appears in $D$; this is easily computed in $O(|D|)$ work. (What about the span?)

So, following that logic, we could come up with a code like this:

$$\sigma$$	$$e'(\sigma)$$
A	0
B	1
C	00
D	11

Is this a valid encoding?

How should we decode 11?

Unambiguous Encoding¶

Instead, we could use:

$$\sigma$$	$$e'(\sigma)$$
A	0
B	10
C	110
D	111

This variable-length encoding is unambiguous.

For our document $D = \langle A, A, A, A, A, A, A, A, A, B, C, D\rangle$, we get the encoding:

$e'(D) = "00000000010110111"$

This has length $1\cdot 9 + 2\cdot 1 + 3\cdot 1 + 3\cdot 1 = 17$. So this is a bit better (we got a length of 24 before).

Optimizing the cost of encoding¶

Given a document $D$ in which we use the alphabet $\Sigma = \{\sigma_1 \ldots \sigma_k\}$, our goal is to create a binary encoding of $\Sigma$ to represent $D$ with as few bits as possible.

In general, the cost of a given encoding $e$ is

$$C(e) = \sum_{i=0}^{|D|} |e(D[i])| = \sum_{\sigma\in\Sigma} f(\sigma)\cdot e(\sigma).$$

Over all possible valid encodings $e: \Sigma \rightarrow \{0,1\}^*$, we want to find a variable-length encoding $e_*$ so that $C(e_*)$ is minimized.

Encodings as Trees¶

How do we ensure that a variable-length encoding is valid? In other words, how do we only consider variable-length encodings that are prefix-free?

We can think of an encoding as representing a tree, with characters from $\Sigma$ as leaves. Note that a fixed-length encoding has all leaves at the same level.

For the two encodings we gave, we'd have:

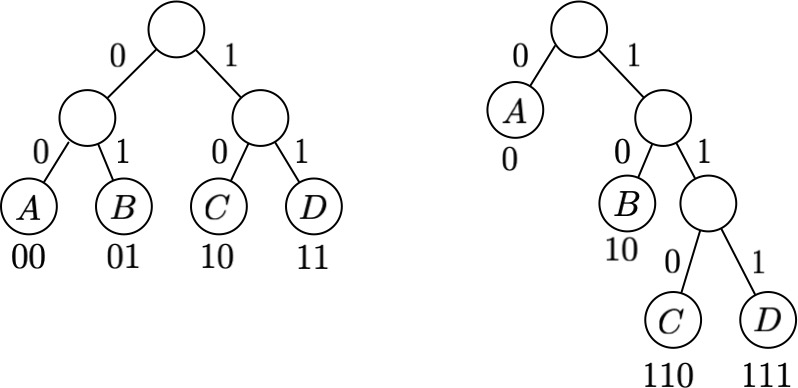
Prefix-free encodings¶

Every prefix-free encoding $e$ can be represented by a tree $T_e$.

The depth of each character $d_T(\sigma)$ in the tree determines how many bits are needed to encode $\sigma$.

So the optimal compression of $D$ can be achieved by identifying the encoding tree $T$ that minimizes:

$$C(T) = \sum_{\sigma\in\Sigma} f(\sigma)\cdot d_T(\sigma)$$

We want to build a prefix-free encoding that is optimal.

Claude Shannon and Robert Fano came up with methods for building prefix-free encodings, but they aren't optimal.

David Huffman (as a graduate student in Fano's class) came up with a bottom-up greedy algorithm to build prefix-free encodings as a class project and was able to prove that it was optimal.

Huffman Coding¶

Intuitively we know we should ensure that when constructing an encoding tree, the higher the frequency, the shorter the path length.

Conversely, the lowest frequency characters should be on the lowest levels.

The main idea of Huffman's algorithm is to choose the two least frequent characters $x$ and $y$ from $\Sigma$ and create a subtree with $x$ and $y$ as sibling leaves for the final encoding.

We then remove $x$ and $y$ from $\Sigma$ and add a new character $z$ with frequency $f(x)+f(y)$, and recurse to compute a tree $T'$.

The final tree $T$ is just $T'$ with $z$ replaced by the subtree with $x, y$ as siblings.

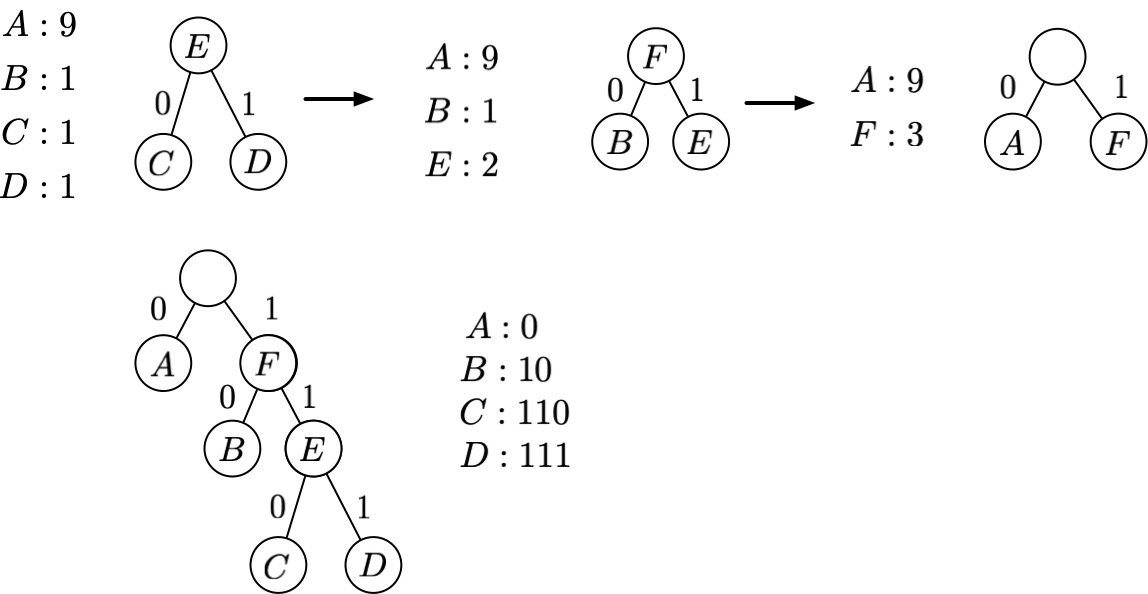
Proof of Optimality¶

Greedy Choice: Let $x, y\in\Sigma$ have the two smallest frequencies ($f(x) \leq f(y)$). Then there is an optimal encoding $T$ for $\Sigma$ with $x, y$ as sibling leaves at maximum depth.

Proof: First let us observe that in an optimal solution $T^*$, $x$ must have maximum depth. Suppose that it did not, and some character $a$ with frequency $f(a)$ had depth $d_{T^*}(a) > d_{T^*}(x)$. Then we can construct a new tree $T^{**}$ by swapping them.

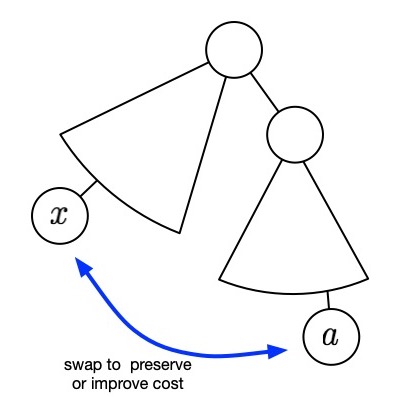
The cost will be:

$\begin{align} C(T^{**}) &=& C(T^*) - f(a)d_{T^*}(a) - f(x)d_{T^*}(x) + f(x)d_{T^*}(a) + f(a)d_{T^*}(x) \\ &=& C(T^*) - (f(a)d_{T^*}(a) + f(x)d_{T^*}(x) - f(x)d_{T^*}(a) - f(a)d_{T^*}(x)) \\ &=& C(T^*) - (f(a)-f(x))(d_{T^*}(a) - d_{T^*}(x)) \\ \end{align}$

If $f(a) > f(x)$ then $C(T^{**}) < C(T^*)$. This is a contradiction.

So this means that we can swap $a$ and $x$ without changing the cost and thus some optimal solution has $x$ as a maximum depth leaf. $\blacksquare$

Why are $x$ and $y$ siblings? Now we can apply the same swapping argument as above to establish that $y$ is a sibling of $x$ in some optimal solution.

Optimal Substructure: Let $\Sigma' = \Sigma - \{x, y\} \cup \{z\}$, where $z\not\in \Sigma$ is a character with frequency $f(z) = f(x) + f(y)$.

If $T'$ is an optimal encoding for $\Sigma'$, then an optimal encoding $T$ for $\Sigma$ can be constructed from $T'$ by replacing the leaf representing $z$ with an internal node that has $x, y$ as children.

Proof: We first make a useful observation of the relationship between the cost of $T$ and $T'$. Observe that:

$\begin{align} C(T) &=& \sum_{\sigma\in\Sigma} f(\sigma)d_T(\sigma) \\ &=& f(x)d_T(x) + f(y)d_T(y) + \sum_{\sigma\in\Sigma - \{x,y\}} f(\sigma)d_T(\sigma) \\ &=& f(x)(1+d_T(z)) + f(y)(1+d_T(z)) + \sum_{\sigma\in\Sigma - \{x,y\}} f(\sigma)d_T(\sigma) \\ &=& (f(x)+f(y))(1+d_T(z)) + \sum_{\sigma\in\Sigma - \{x,y\}} f(\sigma)d_T(\sigma) \\ &=& (f(z))(1+d_T(z)) + \sum_{\sigma\in\Sigma - \{x,y\}} f(\sigma)d_T(\sigma) \\ &=& f(z)+f(z)d_T(z) + \sum_{\sigma\in\Sigma - \{x,y\}} f(\sigma)d_T(\sigma) \\ &=& f(z) + C(T') \\ \end{align}$

Optimal Substructure: Let $\Sigma' = \Sigma - \{x, y\} \cup \{z\}$, where $z\not\in \Sigma$ is a character with frequency $f(z) = f(x) + f(y)$. If $T'$ is an optimal encoding for $\Sigma'$, then an optimal encoding $T$ for $\Sigma$ can be constructed from $T'$ by replacing the leaf representing $z$ with an internal node that has $x, y$ as children.

We've established

$C(T) = f(z) + C(T')$

Suppose that $T$ was not optimal, and that there was some other tree $Z$ with $C(Z) < C(T).$

We can assume that $Z$ must have the two smallest frequency characters as siblings at maximum depth as established above.

Now let's construct $Z'$ by removing $x, y$ and adding $z$ with $f(z) = f(x)+f(y)$.

$Z'$ is an encoding for $\Sigma'$, and we have that $C(Z) = f(z) + C(Z')$.

By our assumption $C(Z) < C(T)$, so $f(z) + C(Z') < f(z) + C(T')$ using the observation above.

But this is a contradiction to the optimality of $T'$ since we now have that $C(Z') < C(T').$

Thus Huffman coding produces an optimal prefix-free encoding. $\blacksquare$

Implementation and Runtime¶

Heaps allow us to efficiently retrieve and insert nodes.

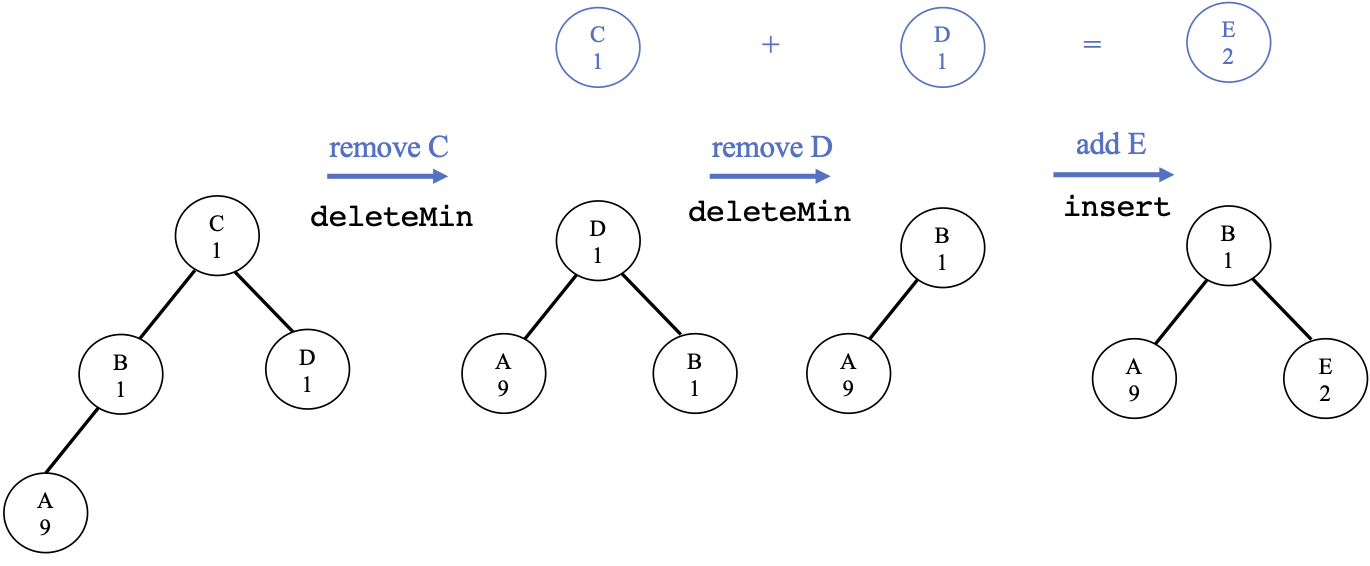
Huffman's Algorithm:

Initialize a min-heap with character frequencies $f(\sigma)$

Then, repeat:

Call deleteMin twice to get the two least frequent nodes $x$ and $y$
Create a new node $z$ with frequency $f(x) + f(y)$
Make $x$ and $y$ children of $z$ in the tree.
Call insert to add $z$ to the heap

Work and Span¶

Huffman's Algorithm

Initialize a min-heap with character frequencies $f(\sigma)$

Then, repeat:

Call deleteMin twice to get the two least frequent nodes $x$ and $y$

Create a new node $z$ with frequency $f(x) + f(y)$

Make $x$ and $y$ children of $z$ in the tree.

Call insert to add $z$ to the heap

Work/span?

Because every iteration reduces the number of nodes by 1, there will be $n$ iterations (where $n = |\Sigma|$).

The cost of 2 calls to deleteMin and one call to insert is $3 \lg n$.

Thus, total work is $O(n \lg n)$.

Span?

No parallelism, so the span is also $O(n \lg n)$.

Decoding¶

So how do we use Huffman coding in practice?

Given a document $D$, we would compute frequencies and then construct an encoding tree $T$. Then to store the compressed version of $D$ we save the encoding of $\Sigma$, the tree $T$ and the encoded version of $D$. To decode a document, we would read bits sequentially and traverse $T$, emitting the appropriate character from $\Sigma$ whenever we hit a leaf.

What is the worst-case work of decoding a document?

$00000000010110111 \rightarrow \langle A, A, A, A, A, A, A, A, A, B, C, D\rangle$

We start at the root, and descend the tree until we reach a leaf.
Then, we return to the root and repeat

So, if the input has $n$ bits, we will visit each bit exactly once.

$\Rightarrow O(n)$

which is equivalent to the total cost of the encoding tree:

$\Rightarrow O(C(T))$

David Huffman invented his coding algorithm as a student in 1951, so it has been around for about 70 years. Yet it is still ubiquitous!

Huffman coding is optimal in the sense that no other prefix code can achieve a shorter average code length. In practice we must identify the best alphabet to use for the coding, i.e., finding the best way to decompose a file into binary "blocks" to get good compression.

Both ZIP and MP3 file formats use Huffman coding as a last step after numerous preprocessing steps.