CMPS 2200¶

Introduction to Algorithms¶

Reduce¶

Agenda:

  • iterate vs reduce
  • sorting with sequences

Reduce¶

A function that repeatedly applies an associative binary operation to a collection of elements until the result is reduced to a single value.

Associative operations can be executed in different orders over the same inputs and give the same output.

  • $plus(plus(2,3), 5) = plus(2, plus(3,5)) = 10$


formal definition of reduce:

$reduce \: (f : \alpha \times \alpha \rightarrow \alpha) (id : \alpha) (a : \mathbb{S}_\alpha) : \alpha$

Input is:

  • $f$: an associative binary function
  • $a$ is the sequence
  • $id$ is the left identity of $f$ $\:\: \equiv \:\:$ $f(id, x) = x$ for all $x \in \alpha$

Returns:

  • a value of type $\alpha$ that is the result of the "sum" with respect to $f$ of the input sequence $a$

When $f$ is associative: $reduce \: f \: id \: a \: \equiv \: iterate \: f \: id \: a$


$reduce \: f \: id \: a = \begin{cases} id & \hbox{if} \: |a| = 0\\ a[0] & \hbox{if} \: |a| = 1\\ f(reduce \: f \: id \: (a[0 \ldots \lfloor \frac{|a|}{2} \rfloor - 1]), \\ \:\:\:reduce \: f \: id \: (a[\lfloor \frac{|a|}{2} \rfloor \ldots |a|-1])& \hbox{otherwise} \end{cases} $

Reduce is a variant of iterate that allows for easier parallelism¶

In [4]:
def reduce(f, id_, a):
    # print('a=%s' % a) # for tracing
    if len(a) == 0:
        return id_
    elif len(a) == 1:
        return a[0]
    else:
        # can call these in parallel
        return f(reduce(f, id_, a[:len(a)//2]),
                 reduce(f, id_, a[len(a)//2:]))
        
def times(x, y):
    return x * y

reduce(times, 1, [1,2,4,6,8])
Out[4]:
384

Work and Span of reduce?¶

Assuming that $f(n)$ has $O(1)$ work and span as times does above:

$$W(n) = 2W(n/2) + 1$$$$S(n) = S(n/2) + 1$$
$$W(n) \in O(n)$$$$S(n) \in O(\lg n)$$

Compare with iterate; sometimes called "left folding"¶

In [3]:
def iterate(f, x, a):
    if len(a) == 0:
        return x
    else:
        return iterate(f, f(x, a[0]), a[1:])
    
iterate(times, 1, [1,2,4,6,8])
Out[3]:
384

Work and Span of iterate?

$$W(n) = W(n-1) + 1$$$$S(n) = S(n-1) + 1$$
$$W(n), S(n) \in O(n)$$

Does order matter?¶

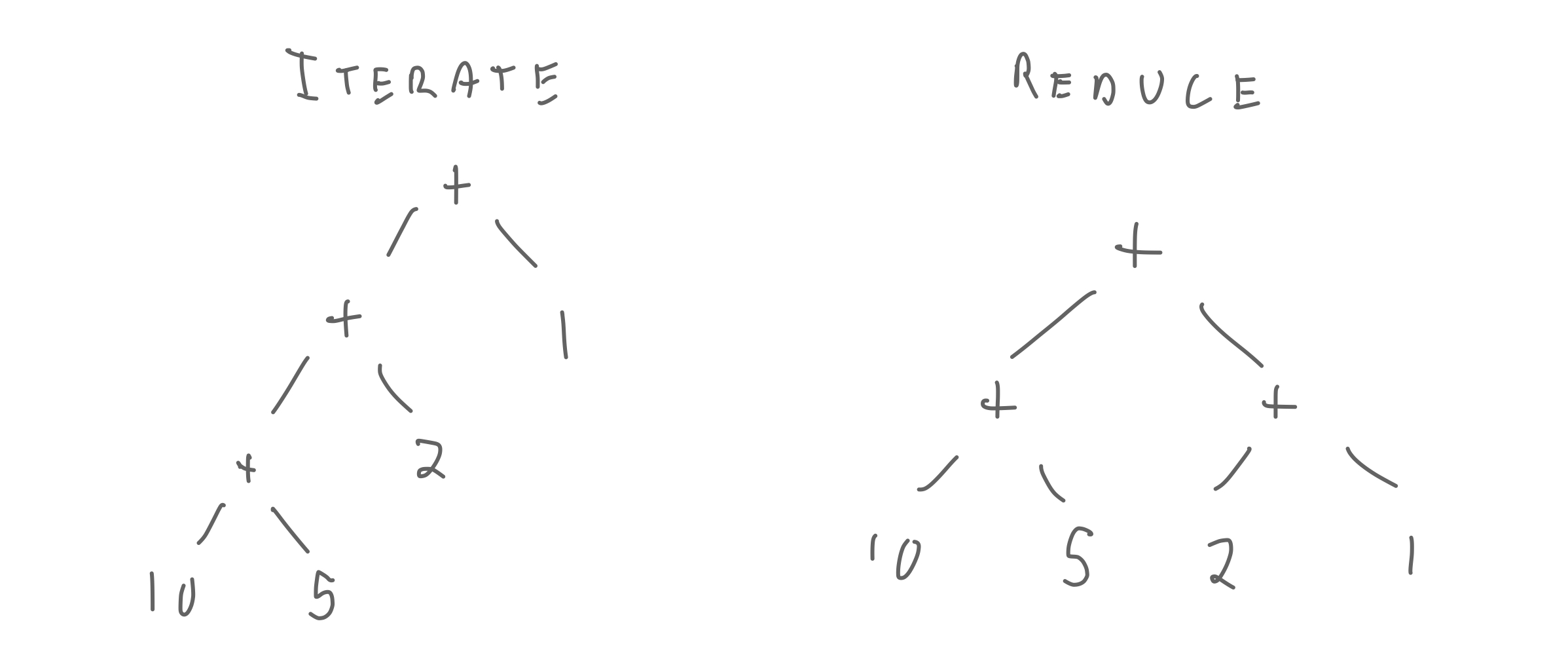
For what function $f$ would $iterate$ and $reduce$ return different answers?

return iterate(f, f(x, a[0]), a[1:])

vs

return f(reduce(f, id_, a[:len(a)//2]),
         reduce(f, id_, a[len(a)//2:])

In [19]:
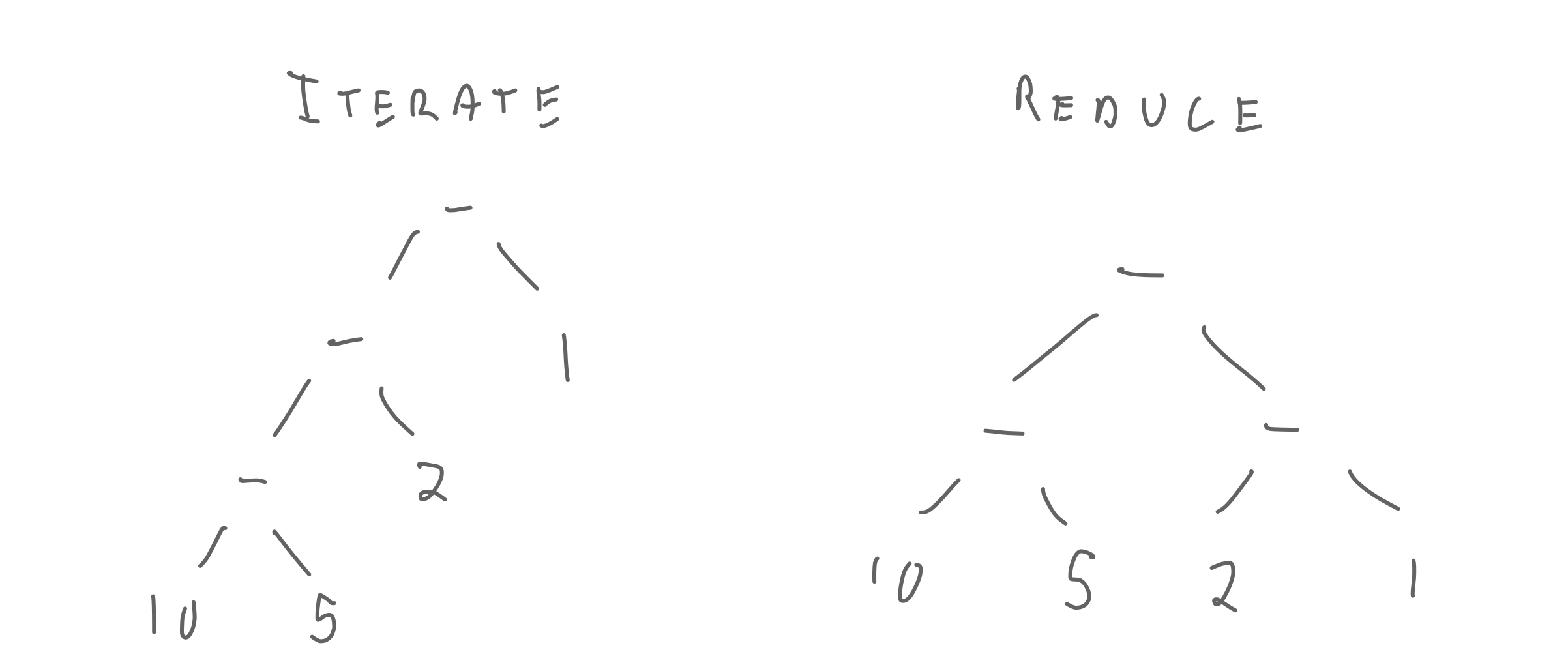
def subtract(x, y):
    return x - y

print(iterate(subtract, 0, [10,5,2,1]))

print(reduce(subtract, 0, [10,5,2,1]))

-18
4

So, why use reduce?

  • Unlike iterate, which is strictly sequential, reduce is parallel.
    • Span of iterate is linear; span of reduce is logarithmic.
    • (we'll cover this later)

Many divide and conquer algorithms can be expressed with reduce.


Recall sum_list_recursive:

In [5]:
# recursive, serial
def sum_list_recursive(mylist):    
    if len(mylist) == 1:
        return mylist[0]
    return (
        sum_list_recursive(mylist[:len(mylist)//2]) +
        sum_list_recursive(mylist[len(mylist)//2:])
    )

sum_list_recursive(range(10))

plus = lambda x,y: x+y
reduce(plus, 0, range(10))
Out[5]:
45

How can we specify this with reduce?

In [11]:
def plus(x, y):
    return x + y

reduce(plus, 0, range(10))
Out[11]:
45

For more complicated combination functions, we can define a generic version of most divide and conquer algorithms and show that it can be implemented with reduce and map.

In [ ]:
## Generic divide and conquer algorithm.

def my_divide_n_conquer_alg(mylist):    
    if len(mylist) == 0:
        return LEFT_IDENTITY# <identity>
    elif len(mylist) == 1:
        return BASECASE(mylist[0]) # basecase for 1
    else:
        return COMBINE_FUNCTION(
            my_divide_n_conquer_alg(mylist[:len(mylist)//2]),
            my_divide_n_conquer_alg(mylist[len(mylist)//2:])
        )

def COMBINE_FUNCTION(solution1, solution2):
    """ return the combination of two recursive solutions"""
    pass

def BASECASE(value):
    """ return the basecase value for a single input"""
    pass

### is equivalent to
reduce(COMBINE_FUNCTION, LEFT_IDENTITY, (map(BASECASE, mylist)))

Example: Sorting with Reduce¶

In [3]:
def merge(left, right):
    """
    Takes in two sorted lists and returns a sorted list that combines them both.
    """
    i = j = 0
    result = []
    while i < len(left) and j < len(right):
        if right[j] < left[i]:   # out of order: e.g., left=[4], right=[3]
            result.append(right[j])
            j += 1
        else:                   # in order: e.g., left=[1], right=[2]
            result.append(left[i])
            i += 1    
    # append any remaining items (at most one list will have items left)
    result.extend(left[i:])
    result.extend(right[j:])
    return result

merge([1,4,8], [2,3,10])
Out[3]:
[1, 2, 3, 4, 8, 10]

What is base case and left identity?

In [5]:
def singleton(value):
    """ create a list with one element. """
    return [value]

## reduce(COMBINE_FUNCTION, LEFT_IDENTITY, (map(BASECASE, mylist)))
reduce(merge, [], list(map(singleton, [1,3,6,4,8,7,5,2])))
Out[5]:
[1, 2, 3, 4, 5, 6, 7, 8]
In [6]:
list(map(singleton, [1,3,6,4,8,7,5,2]))

#[[val] for val in [1,3,6,4,8,7,5,1]]
Out[6]:
[[1], [3], [6], [4], [8], [7], [5], [2]]

What if we use iterate instead of reduce?

In [30]:
iterate(merge, [], list(map(singleton, [1,3,6,4,8,7,5,2])))
Out[30]:
[1, 2, 3, 4, 5, 6, 7, 8]

Order matters¶

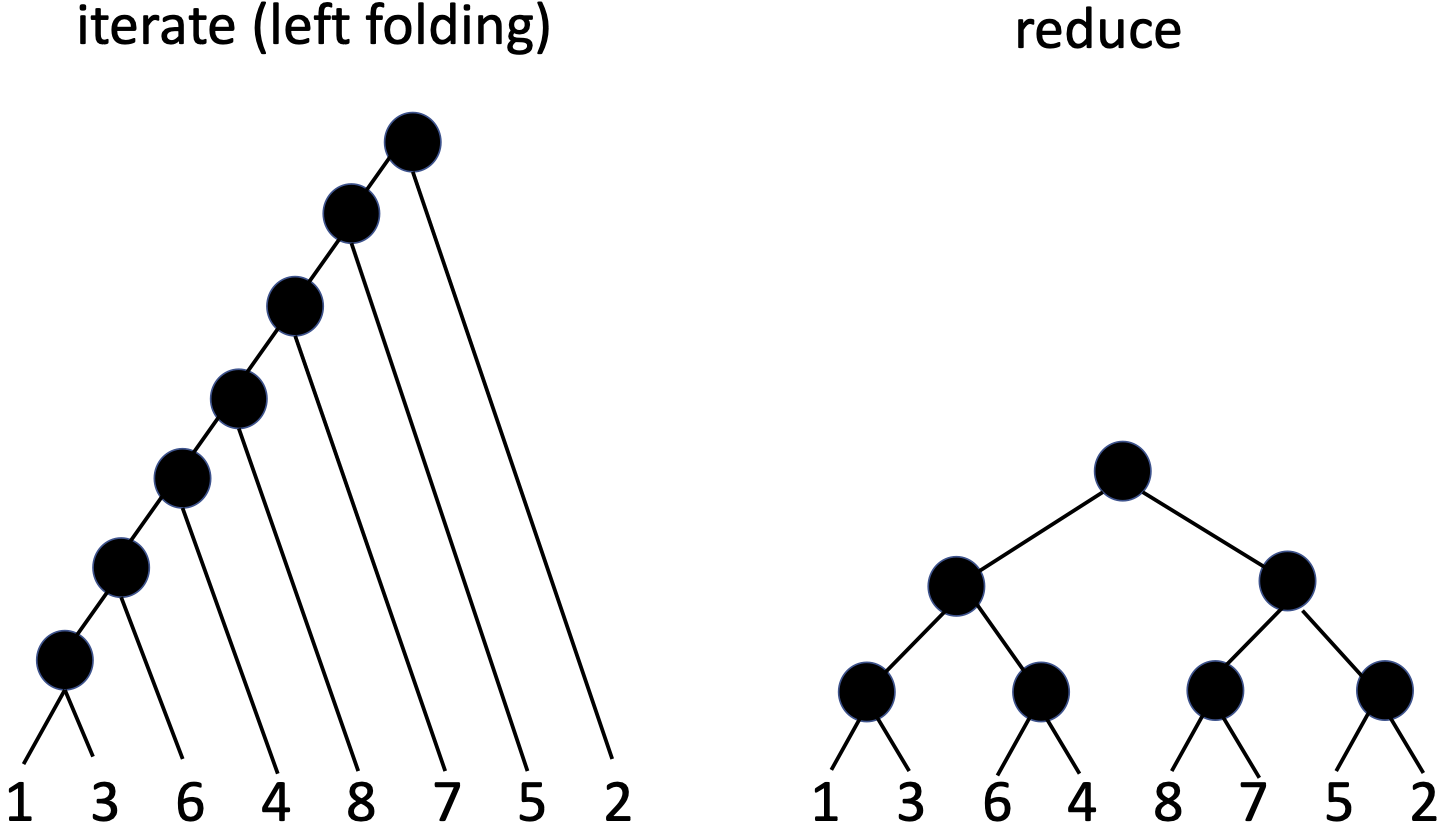
order

Analysis¶

iterate(merge, [], list(map(singleton, [1,3,6,4,8,7,5,2])))

This is insertion sort!

  • We iterate from left to right.
  • At each step we insert the next element into the appropriate place in the sorted list.

$[1] \rightarrow [1,3] \rightarrow [1,3,6] \rightarrow [1,3,4,6] \ldots$



Assuming the merge function has work $O(n)$.

$$W(n) = W(n-1) + n \in O(n^2)$$



Assuming the merge function has span $O(\lg n)$ (note our implementation above doesn't do this).

$$S(n) = S(n-1) + \lg n \in O(n \lg n)$$

reduce(merge, [], list(map(singleton, [1,3,6,4,8,7,5,2])))

This is merge sort!



Assuming the merge function has work $O(n)$.

$$W(n) = 2W(n/2) + n \in O(n \lg n)$$

Assuming the merge function has span $O(\lg n)$.

$$S(n) = S(n/2) + \lg n \in O(\lg^2 n)$$

Map-Reduce¶

Scalable, parallel programming model popularized by Google.

It is used to parallelize the processing of large datasets across clusters of computers.

It consists of four basic steps:

  1. Split the data in trivial key-value pairs, somewhat analogous to base cases
    • In this step we are mapping each piece of data to some value, returning a list of all key-value pairs.
  2. Collect all values for the same keys into lists.
    • Results in a collection of tuples, one for each key. The value for each key is now a list of all the values for that key from the previous step
  3. Reduce the values for each key into a single data point
    • this can be in parallel
  4. Return a list of all processed key value pairs
In [ ]:
def run_map_reduce(map_f, reduce_f, docs):
    """    
    The main map reduce logic.
    
    Params:
      map_f......the mapping function
      reduce_f...the reduce function
      docs.......list of input records
    """
    # 1. call map_f on each element of docs and flatten the results
    # e.g., [('i', 1), ('am', 1), ('sam', 1), ('i', 1), ('am', 1), ('sam', 1), ('is', 1), ('ham', 1)]
    pairs = flatten(list(map(map_f, docs)))
    # 2. group all pairs by their key
    # e.g., [('am', [1, 1]), ('ham', [1]), ('i', [1, 1]), ('is', [1]), ('sam', [1, 1])]
    groups = collect(pairs)
    # 3. reduce each group to the final answer
    # e.g., [('am', 2), ('ham', 1), ('i', 2), ('is', 1), ('sam', 2)]
    return [reduce_f(g) for g in groups]

Example¶

Suppose we are counting the frequencies of words in some text. This is a common task in the field of natural language processing.

Here is our corpus:

"left foot left foot"
"right foot right"
"wet foot dry foot"
"high foot low foot"

Step 1: Split it into all words, mapping each to a frequency of 1. There will be repeated words.

[('left', 1), ('foot', 1), ('left', 1), ('foot', 1), ('right', 1), ('foot', 1), ('right', 1), ('wet', 1), ('foot', 1), ('dry', 1), ('foot', 1), ('high', 1), ('foot', 1), ('low', 1), ('foot', 1)]

Step 2: Collect all values for the same word into individual lists.

[('dry', [1]), ('foot', [1, 1, 1, 1, 1, 1, 1]), ('high', [1]), ('left', [1, 1]), ('low', [1]), ('right', [1, 1]), ('wet', [1])]

Step 3: Run reduce on every tuple above to sum all counts into a final frequency.

[('dry', 1), ('foot', 7), ('high', 1), ('left', 2), ('low', 1), ('right', 2), ('wet', 1)]

Step 4: Return a list of all word frequencies

[('dry', 1), ('foot', 7), ('high', 1), ('left', 2), ('low', 1), ('right', 2), ('wet', 1)]