Agenda:
- Learn what sequences are and what primitive operators we can compute with them.
- Use these primitive operators to solve several problems efficiently and in parallel.
Abstract Data Types¶
interface consisting of a collection of functions (and possibly values) on a given type, without reference to the implementation
distinguished from a data structure, which contains the actual implementations.
ADT: what
Data Structure: how
ADT often also includes cost specification (e.g., value lookup is $O(1)$, search is $O(n)$, etc).
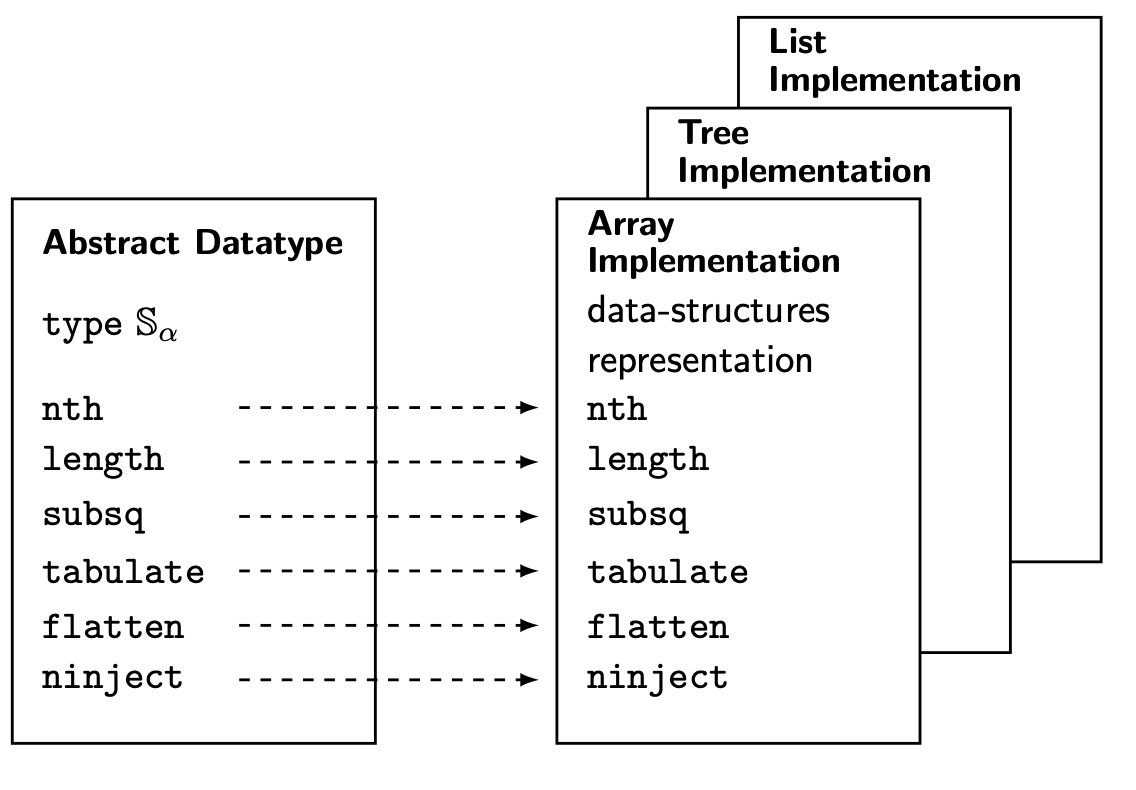
how to choose the "right" implementation?¶
Sequences¶
- one of the most popular, common ADTs
- many useful functions for parallel algorithms
Simple to express by example:
$\langle 10, 20, 40 \rangle$
We'll spend some time defining it more formally so the semantics are precise.
We'll then define primitive operations over sequences that can be composed to solve a wide array of problems involving sequences.
First, a quick refresher of sets, relations, and functions...
Set¶
set: collection of distinct objects
- each element of a set appears exactly once
- set with no elements is empty set: $\{\}$ or $\emptyset$
- can be specified by a set comprehension
E.g., Cartesian product of sets $A$ and $B = \{(i,j) : i \in A, j \in B\}$
- " tuples $i$ and $j$ such that $i$ is in $A$ and $j$ is in $B$ "
Relation¶
A binary relation $R$ from a set $A$ to a set $B$ is a subset of the Cartesian product of $A$ and $B$.
- $R \subseteq A \times B$
- domain of $R$ is the set $\{a : (a,b) \in R\}$
- range of $R$ is the set $\{b : (a,b) \in R\}$
Function¶
A function or mapping from $A$ to $B$ is a relation $R \subset A \times B$ such that:
- $|R| = |$domain$(R)|$
- that is, for every $a$ in the domain of $R$, there is only one $b$ in the range of $R$ such that $(a,b) \in R$
$A$ is the domain and $B$ is the co-domain.
Sequence¶
A sequence is a function whose domain is a contiguous set of natural numbers starting at zero.
An $\alpha$ sequence is a function from $\mathbb{N}$ to $\alpha$ with domain $\{0, \ldots, n-1\}$ for some $n \in \mathbb{N}$
- $\alpha$ specifies the type of the sequence elements
E.g., $X$ and $Y$ are equivalent sequences:
$ X = \{(0, $ '$a$'$), (1, $ '$b$'$), (2, $ '$c$'$)\} \equiv \langle $'$a$'$, \: $'$b$'$, \: $'$c$'$\rangle$
$ Y = \{(1, $ '$b$'$), (2, $ '$c$'$), (0, $ '$a$'$)\} \equiv \langle $'$a$'$, \: $'$b$'$, \: $'$c$'$\rangle$
$Z$ is not a sequence. why not?
$ Z = \{(0, $ '$a$'$), (2, $ '$c$'$)\} $
does not have domain $\{0, \ldots, n-1\}$
Next, we'll define a number of functions over sequences and use them to solve problems.
For each, we'll show the mathematical definition, SPARC syntax, and python code.
Tabulate¶
$tabulate$ is a function that takes as input:
- another function $f$
- a natural number $n$
and returns a sequence of length $n$ by applying $f$ to each element in $\langle 0, \ldots, n-1 \rangle$
formal definition:
$tabulate \: (f : \: \mathbb{N} \rightarrow \alpha)\: (n :\: \mathbb{N}) : \: \mathbb{S}_\alpha = \langle f(0), f(1), \ldots, f(n-1) \rangle$
SPARC syntax:
$tabulate \: (\mathtt{lambda} \: i \: . \: e)\: e_n \equiv \langle e : \: 0 \le i < e_n \rangle $
- the second expression is a sequence comprehension
- $e_n$ is a SPARC expression whose value is a natural number
e.g.
$tabulate \: fib \:\: 9 \equiv \langle fib \: i : \: 0 \le i < 9 \rangle \Rightarrow \langle 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 \rangle$
def tabulate(f, n):
return [f(i) for i in range(n)]
tabulate(lambda x: x**2, 10)
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
Each call to $f(i)$ can be done in parallel!¶
from multiprocessing.pool import ThreadPool
def parallel_tabulate(f, n, nthreads=5):
with ThreadPool(nthreads) as pool:
results = []
# launch all tasks
for i in range(n):
results.append(pool.apply_async(f, [i]))
# wait for all to finish
return [r.get() for r in results]
list(parallel_tabulate(lambda x: x**2, 10))
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
Map¶
- like $tabulate$, but applies $f$ to elements of sequence, rather than integers.
$map$ is a function that takes as input:
- another function $f : \alpha \rightarrow \beta$
- a sequence $a$ of type $\mathbb{S}_\alpha$
and returns a sequence of type $\mathbb{S}_\beta$ with length $n$ by applying $f$ to each element $x \in a$
formal definition:
$ map \: (f : \alpha \rightarrow \beta)(a : \mathbb{S}_\alpha) : \mathbb{S}_\beta = \{(i, f(x)) : (i, x) \in a\}$
SPARC syntax:
$\langle e : p \in e_s \rangle \equiv map\:(\mathtt{lambda} \: p \: . \: e)\: e_s$
e.g., assume $a = \langle 2, 4, 5, 7\rangle$
$map\: (\mathtt{lambda} \: x \: . \: x^2)\: a \equiv \langle x^2 : x \ \in a \rangle \Rightarrow \langle 4, 16, 25, 49 \rangle$
def my_map(f, a):
return [f(x) for x in a]
my_map(lambda x: x**2, [4, 16, 25, 49])
[16, 256, 625, 2401]
# In fact, map is built into python:
list(map(lambda x: x**2, [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31]))
[4, 9, 25, 49, 121, 169, 289, 361, 529, 841, 961]
Filter¶
like $map$, but $f$ is a boolean function, and the returned list contains elements where $f(x)$ is True.
$filter$ is a function that takes as input:
- another function $f : \alpha \rightarrow \mathbb{B}$
- a sequence $a$ of type $\mathbb{S}_\alpha$
and returns a sequence of type $\mathbb{S}_\alpha$ with length $\le n$ by applying $f$ to each element $x \in a$ and retaining only those where $f(x)$ is $\mathtt{True}$, while preserving the relative order of the elements returned.
formal definition:
(convoluted because we have to preserve the relative order of the elements)
$ filter \: (f : \alpha \rightarrow \mathbb{B})(a : \mathbb{S}_\alpha) : \mathbb{S}_\alpha = \{\: (\: \vert \: \{(j,y) \in a | j < i \land f(y)\} \: \vert, \: x) : (i,x) \in a | f(x) \: \}$
SPARC syntax:
$\langle x \in e_s \: \vert \: e \rangle \equiv filter\:(\mathtt{lambda}\: x \: . \: e)\: e_s$
e.g., assume $a = \langle 2, 4, 5, 7\rangle$
$filter\: \mathtt{isEven} \: a \equiv \langle x : x \in a \: \vert \: \mathtt{isEven}\: x \rangle \Rightarrow \langle 2, 4\rangle$
def my_filter(f, a):
return [x for x in a if f(x)]
my_filter(lambda x: x%2==0, [4, 16, 25, 49])
[4, 16]
# like map, this also already exists...
list(filter(lambda x: x%2==0, [4, 16, 25, 49]))
[4, 16]
Collect¶
Given a sequence of key-value pairs, the operation collect “collects” together all the values for a given key.
It takes in a sequence of tuples which are the key-value pairs and returns a sequence of tuples, one tuple for key with its value being a sequence of all the values that key maps to.
Example:
$ \begin{align} kv = \langle &(\text{'}\,{\texttt{jack}}\,\text{'}, \text{'}\,{\texttt{15210}}\,\text{'}), (\text{'}\,{\texttt{jack}}\,\text{'}, \text{'}\,{\texttt{15213}}\,\text{'}) \\ &(\text{'}\,{\texttt{mary}}\,\text{'}, \text{'}\,{\texttt{15210}}\,\text{'}), (\text{'}\,{\texttt{mary}}\,\text{'}, \text{'}\,{\texttt{15213}}\,\text{'}), (\text{'}\,{\texttt{mary}}\,\text{'}, \text{'}\,{\texttt{15251}}\,\text{'}), \\ &(\text{'}\,{\texttt{peter}}\,\text{'}, \text{'}\,{\texttt{15150}}\,\text{'}), (\text{'}\,{\texttt{peter}}\,\text{'}, \text{'}\,{\texttt{15251}}\,\text{'}), \\ &\ldots \\ &\rangle. \end{align} $
$ \begin{align} \mathit{collect}~\mathit{cmp}~kv = \langle &(\text{'}\,{\texttt{jack}}\,\text{'}, \left\langle\, \text{'}\,{\texttt{15210}}\,\text{'}, \text{'}\,{\texttt{15213}}\,\text{'}, \ldots \,\right\rangle) \\ &(\text{'}\,{\texttt{mary}}\,\text{'}, \left\langle\, \text{'}\,{\texttt{15210}}\,\text{'}, \text{'}\,{\texttt{15213}}\,\text{'}, \text{'}\,{\texttt{15251}}\,\text{'}, \ldots \,\right\rangle), \\ &(\text{'}\,{\texttt{peter}}\,\text{'}, \left\langle\, \text{'}\,{\texttt{15150}}\,\text{'}, \text{'}\,{\texttt{15251}}\,\text{'}, \ldots \,\right\rangle), \\ &\ldots \\ &\rangle . \end{align} $
$\mathit{cmp}$ is a comparison operator over the keys of the tuples. The collected sequence is sorted in order by the keys. The values appear in the same order as they did in the input sequence.
def collect(pairs):
"""
Implements the collect function
E.g.:
>>> collect([('i', 1), ('am', 1), ('sam', 1), ('i', 1)])
[('am', [1]), ('i', [1, 1]), ('sam', [1])]
"""
result = defaultdict(list)
for pair in sorted(pairs):
result[pair[0]].append(pair[1])
return list(result.items())
Note that collect depends on sorted, a $\Theta(n \lg n)$ operation.
Append¶
- $append(a,b)$ appends sequence $b$ after sequence $a$
- shorthand: $a +\!\!+ \: b$
- e.g., $\langle 1,2,3 \rangle +\!\!+ \: \langle 4, 5 \rangle \Rightarrow \langle 1,2,3,4,5 \rangle $
Flatten¶
- append two or more sequences.
- $flatten \langle \langle 1,2,3 \rangle, \langle 4 \rangle, \langle 5, 6 \rangle \rangle \Rightarrow \langle 1,2,3,4,5,6 \rangle$
Update¶
- $update (a, (i, x))$ updates location $i$ of sequence $a$ to have value $x$
- e.g., $a = \langle 1,2,3,4,5,6 \rangle$
- $update \: a \: (2, 99) \Rightarrow \langle 1,2,\mathbf{99},4,5,6 \rangle$
- How can we ensure data persistence here?
Inject¶
- update multiple locations at once
- e.g., $a = \langle 1,2,3,4,5,6 \rangle$
- $inject \: a \: \langle (2, 99), (4, 100) \rangle \Rightarrow \langle 1,2,\mathbf{99},4, \mathbf{100}, 6 \rangle $
- what if we want to parallelize $inject$?
Nondeterministic Inject¶
Can we just parallelize each update?
$a = \langle 1,2,3,4,5,6 \rangle$
$inject \: a \: \langle (2, 99), (2, 100) \rangle \Rightarrow $ ???
$ninject \: a \: \langle (2, 99), (2, 100) \rangle \Rightarrow$
$\langle 1,2,\mathbf{99},4,5,6 \rangle$ OR $\langle 1,2,\mathbf{100},4,5,6 \rangle$
essentially ignore race conditions
Iterate¶
Iterate over a sequence and accumulate a result that changes at each step (e.g., "running sum")
$iterate \ (f : \alpha \times \beta \rightarrow \alpha) (x : \alpha) (a : \mathbb{S}_\beta) : \alpha$
$iterate$ is a function that takes as input:
- another function $f : \alpha \times \beta \rightarrow \alpha$
- an initial result $x$
- a sequence $a$ of type $\mathbb{S}_\beta$
and returns a value of type $\alpha$ that is the result of applying $f(x,a)$ to each element of the sequence.
$iterate \: f \: x \: a = \begin{cases} x & \hbox{if} \: |a| = 0\\ iterate \: f \:\: f(x, a[0]) \:\:\: a[1 \ldots |a|-1]& \hbox{otherwise} \end{cases} $
e.g.
$iterate \:\: + \:\:\: 0 \:\:\: \langle 2,5,1,6 \rangle \Rightarrow (((2+5)+1)+6) \Rightarrow 14$
$f(f(f(x, a[0]), a[1]), a[2])\ldots)$
def iterate(f, x, a):
"""
Params:
f.....function to apply
x.....return when a is empty
a.....input sequence
"""
print('iterate: calling %s x=%s a=%s' % (f.__name__, x, a))
if len(a) == 0:
return x
else:
return iterate(f, f(x, a[0]), a[1:])
def plus(x, y):
return x + y
iterate(plus, 0, [2,5,1,6])
iterate(lambda x,y: x*y, 1, [2,3,5,7,11,13,17,19])
How can we use iterate to implement flatten?¶
- $flatten \langle \langle 1,2,3 \rangle, \langle 4 \rangle, \langle 5, 6 \rangle \rangle \Rightarrow \langle 1,2,3,4,5,6 \rangle$
def flatten(sequences):
return iterate(plus, [], sequences)
flatten([[1,2,3], [4], [5,6]])
iterate: calling plus x=[] a=[[1, 2, 3], [4], [5, 6]] iterate: calling plus x=[1, 2, 3] a=[[4], [5, 6]] iterate: calling plus x=[1, 2, 3, 4] a=[[5, 6]] iterate: calling plus x=[1, 2, 3, 4, 5, 6] a=[]
[1, 2, 3, 4, 5, 6]
Iterate Prefixes¶
- also returns the intermediate values computed by $iterate$
$ iteratePrefixes \: f \: x \: a = \\ ~~\mathtt{let} \: g (b,x)\: y = (b +\!\!+x, f(x,y))\\ ~~\mathtt{in} \: iterate\: g (\langle \rangle, x)\: a \: \mathtt{end} $
def iterate(f, x, a):
#print('iterate: calling %s x=%s a=%s' % (f.__name__, x, a))
if len(a) == 0:
return x
else:
return iterate(f, f(x, a[0]), a[1:])
def iterate_prefixes(f, x, a):
def g(result, next_element):
prefixes, current_result = result[0], result[1]
#print('\titerate_prefixes: prefixes=%s current_result=%s next_element=%s\n' % (prefixes, current_result, next_element))
# get next result
r = f(current_result, next_element)
return (prefixes + [r], r)
return iterate(g, ([], x), a)
print(iterate_prefixes(lambda x,y: x*y, 1, [2,3,5,7,11,13,17,19]))
([2, 6, 30, 210, 2310, 30030, 510510, 9699690], 9699690)
Problem: Rightmost Positive¶
Given a sequence of integers $a$, for each element in $a$ find the rightmost positive number to its left.
E.g.,
$rpos \: \langle 1, 0, -1, 2, 3, 0, -5, 7 \rangle \Rightarrow \langle -\infty, 1, 1, 1, 2, 3, 3, 3 \rangle$
($-\infty$ if no positive element to the left)
Let's design a solution using $iterate$
import math
def extend_positive(result, next_element):
"""
Params:
result.........tuple of (last positive value, list of intermediate outputs)
next_element...next element to be read from input list
Returns:
tuple of (last positive value, list of intermediate outputs)
"""
last_positive_value, sequence = result[0], result[1]
new_sequence = sequence + [last_positive_value] # data persistence...vs. sequence.append(last_positive_value)
if next_element > 0:
return (next_element, new_sequence) # next_element becomes the last_positive_value
else:
return (last_positive_value, new_sequence) # last_positive_value is unchanged
# call extend_positive for each element of input [1,0,-2,...]
result1 = extend_positive( (-math.inf, []), 1)
print(result1)
result2 = extend_positive( result1, 0)
print(result2)
result3 = extend_positive( result2, -1)
print(result3)
result4 = extend_positive( result3, 2)
print(result4)
result5 = extend_positive( result4, 3)
print(result5)
(1, [-inf]) (1, [-inf, 1]) (1, [-inf, 1, 1]) (2, [-inf, 1, 1, 1]) (3, [-inf, 1, 1, 1, 2])
iterate(extend_positive, (-math.inf, []), [1,0,-1,2,3,0,-5,7])
iterate: calling extend_positive x=(-inf, []) a=[1, 0, -1, 2, 3, 0, -5, 7] iterate: calling extend_positive x=(1, [-inf]) a=[0, -1, 2, 3, 0, -5, 7] iterate: calling extend_positive x=(1, [-inf, 1]) a=[-1, 2, 3, 0, -5, 7] iterate: calling extend_positive x=(1, [-inf, 1, 1]) a=[2, 3, 0, -5, 7] iterate: calling extend_positive x=(2, [-inf, 1, 1, 1]) a=[3, 0, -5, 7] iterate: calling extend_positive x=(3, [-inf, 1, 1, 1, 2]) a=[0, -5, 7] iterate: calling extend_positive x=(3, [-inf, 1, 1, 1, 2, 3]) a=[-5, 7] iterate: calling extend_positive x=(3, [-inf, 1, 1, 1, 2, 3, 3]) a=[7] iterate: calling extend_positive x=(7, [-inf, 1, 1, 1, 2, 3, 3, 3]) a=[]
(7, [-inf, 1, 1, 1, 2, 3, 3, 3])
In SPARC:
\begin{array}{l} \mathit{extendPositive}~((\ell, b), x) = \\ ~~~~\texttt{if}~x > 0~\texttt{then}\\ ~~~~~~~~(x, b +\!\!+{} \left\langle\, \ell \,\right\rangle) \\ ~~~~\texttt{else} \\ ~~~~~~~~(\ell, b +\!\!+{} \left\langle\, \ell \,\right\rangle) \end{array}Can we solve $\mathtt{RightmostPositive}$ using iteratePrefixes instead?
First we need to define the function to apply.
def select_positive(last_positive_value, next_element):
"""
Params:
last_positive_value...the last positive value seen
next_element..........next element from input list
Returns:
the element to be remembered going forward
"""
if next_element > 0: # remember this new value
return next_element
else: # reuse the old value
return last_positive_value
# no need to keep track of the return sequence as in extend_positive
# we let iterate_prefixes handle that.
iterate_prefixes(select_positive, -math.inf, [1,0,-1,2,3,0,-5,7])
In SPARC
\begin{array}{l} \mathit{selectPositive}~(\ell, x) = \\ ~~~~\texttt{if}~x > 0~\texttt{then}\\ ~~~~~~~~x \\ ~~~~\texttt{else} \\ ~~~~~~~~\ell \end{array}Much less code!
- These functions are powerful primitives that can be composed into more complicated algorithms.