Recap¶
Recurrences allow us to express the runtime of any algorithm.
$$T(n) = a \cdot T(\frac{n}{b}) + f(n)$$- $a$ is the branching factor.
- $\frac{n}{b}$ gives us the sub-problem size at the next level.
- $f(n)$ is the cost of the work (or span) within each recursive call.
Key Idea: Recurrences can be drawn as recursion trees. The total cost of a recurrence is the sum of the costs over the entire tree.
Example
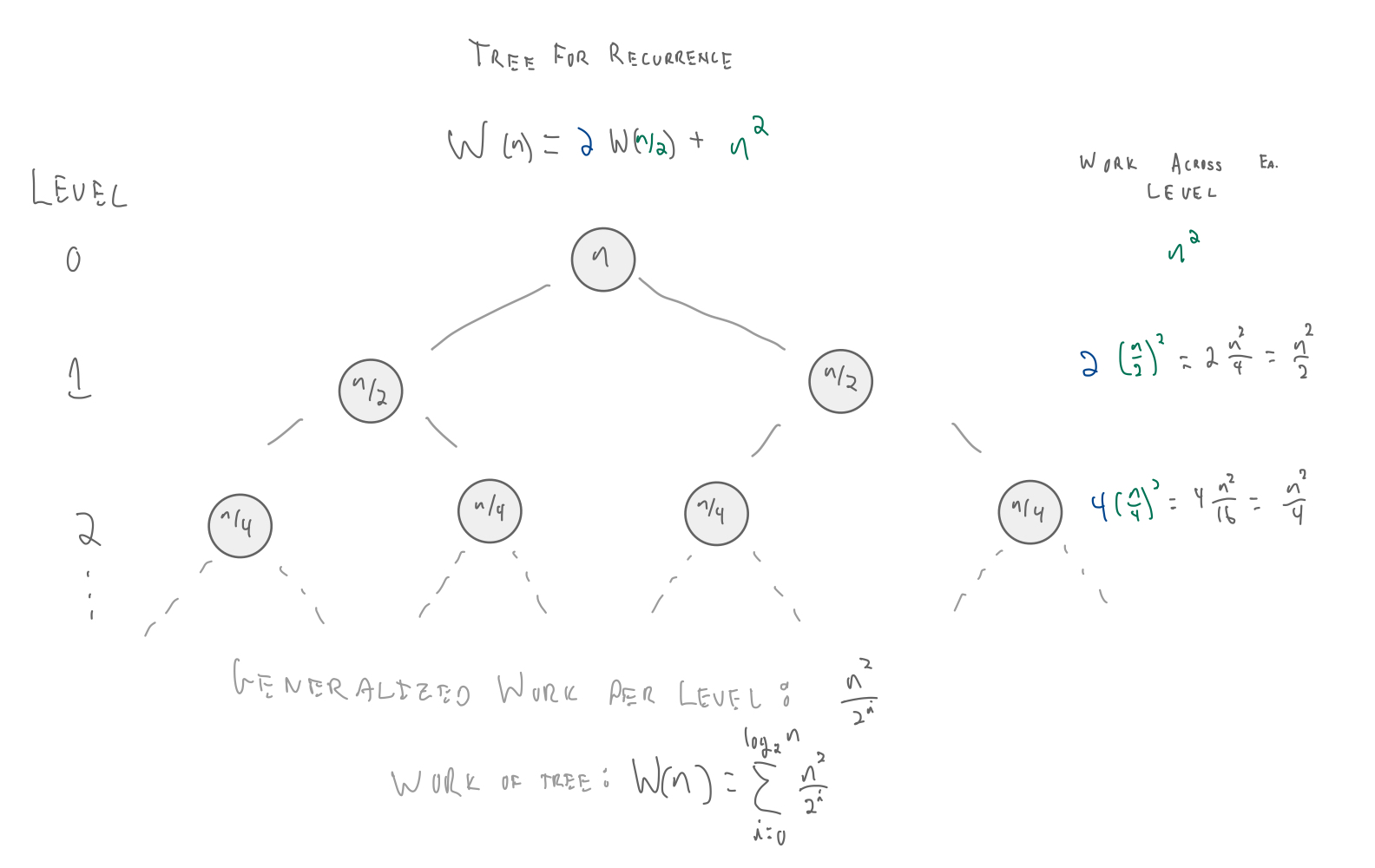
Generalizing Recurrence Solutions¶
There are often patterns in the costs down the levels of a tree.
We will examine and use these patterns to our benefit.
The brick method gives a way to derive asymptotic runtimes by looking at the relationships between parent and child nodes in the recursion tree.
The Brick Method¶
In recursion trees, if the costs grow or decay geometrically across levels, then we need only consider the cost of the root (if they decay), or the total cost of the leaves (if they grow).
If there is no growth or decay then we can calculate the cost of the worst level (often either the root or leaves) and multiply it by the number of levels.
This leads to three cases:
- root dominated
- leaf dominated
- balanced
Conveniently, to distinguish these three cases we need only consider the cost of each node in the tree and how it relates to the cost of its children.
Geometric Series Recap¶
The value of $n$ decreases geometrically as we collect the terms in our recurrences. We'll make use of bounds for geometric series.
For any $\alpha > 1$:
$$ \sum_{i=0}^n \alpha^i \lt \frac{\alpha}{\alpha - 1}\cdot\alpha^n$$For $\alpha < 1$:
$$ \sum_{i=0}^\infty \alpha^i \lt \frac{1}{1-\alpha}$$Root-dominated¶
For a node $v$ in the recursion tree, let $C(v)$ denote its cost and $D(v)$ denote its children.
A recurrence is root-dominated if for all $v$, there is an $\alpha > 1$ such that:
$$C(v) \geq \alpha \sum_{u \in D(v)} C(u)$$The cost of node $C(v)$ is larger than the cost of its children by a geometric factor.
The cost of a root dominated recurrence is $O(C(r))$ if $r$ is the root.
This is because the cost reduces geometrically as we go toward the leaves, and the total cost bounded by $\alpha/(\alpha-1)$ times $C(r)$.
Example

$C(\hbox{root}) = n^2$
$C(\hbox{level}\:1) = \Big(\frac{n}{2}\Big)^2 + \Big(\frac{n}{2}\Big)^2 = \frac{n^2}{2}$
Cost has decreased by a factor of two when descending one level in the tree.
so, if $\alpha \leftarrow 2$:
$C(v) \ge \alpha \sum_{u \in D(v)} C(u)$
$n^2 \ge 2 * \frac{n^2}{2}$
$n^2 \ge n^2$
Because the cost is asymptotically dominated by the root, we need to only consider its cost:
$W(n) \in O(n^2)$.
Leaf-dominated¶
A recurrence is leaf-dominated if for all $v$, there is an $\alpha > 1$ such that:
$$C(v) \leq \frac{1}{\alpha} \sum_{u \in D(v)} C(u)$$The cost of node $C(v)$ is smaller by a geometric factor than the cost of its children.
In other words, the cost is increasing geometrically as we go toward the leaves, and the total cost is bounded by $\alpha/(\alpha-1)$ times $c_b \cdot L$.
If we have $L$ leaves in the recursion tree, the cost of a leaf dominated recurrence is $O(L)$.
Example
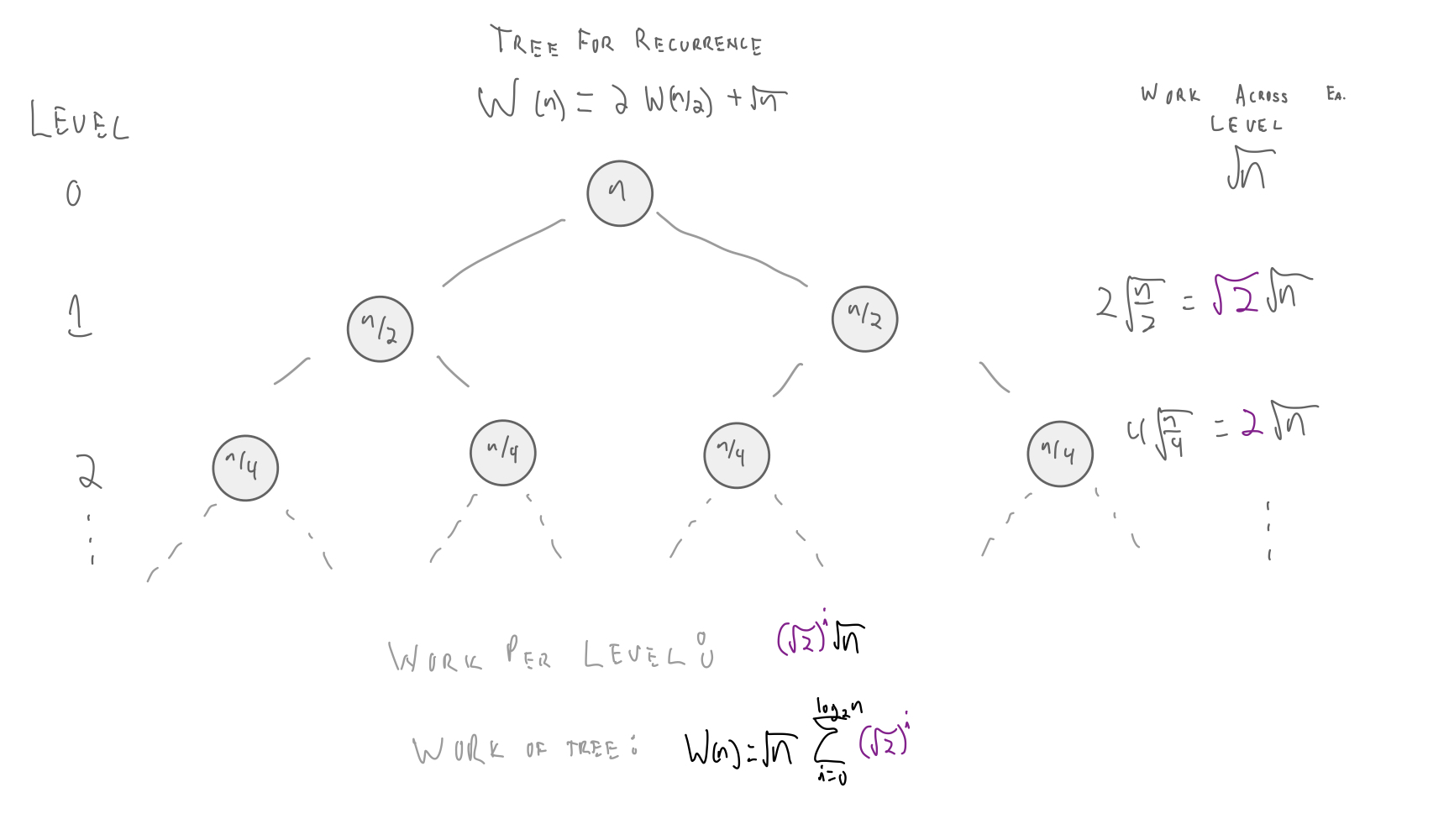
$C(\hbox{root}) = \sqrt{n}$
$C(\hbox{level}\:1) = \sqrt{\Big(\frac{n}{2}\Big)} + \sqrt{\Big(\frac{n}{2}\Big)} = 2 \frac{\sqrt{n}}{\sqrt{2}} = \sqrt{2}\sqrt{n}$
Cost has increased by a factor of $\sqrt{2}$ when descending one level in the tree.
so, if $\alpha \leftarrow \frac{1}{\sqrt{2}}$:
$C(v) \le \frac{1}{\alpha} \sum_{u \in D(v)} C(u)$
$\sqrt{n} \le \frac{1}{\sqrt{2}} * \sqrt{2}\sqrt{n}$
$\sqrt{n} \le \sqrt{n}$
Because the cost is asymptotically dominated by the leaves (i.e., lowest level of the tree), we need to only consider their cost:
- Cost of each leaf is 1 (since $\sqrt{1}==1$).
- Depth of tree is $\lg{n}$ (since we divide by 2 at each level)
- Number of leaves of a binary tree with depth $\lg{n}$ is $2^{\lg{n}} = n$
So, final cost is $W(n) \in O(n)$
More generally, the number of leaves is:
$$a^{\log_b n} = n^{\log_b a}$$Balanced¶
A recurrence is balanced when every level of the recursion tree has the same asymptotic cost. In this case, the recurrence is number of levels ($T_d$ "tree depth") times maximum cost per level ($C_L$).
Example
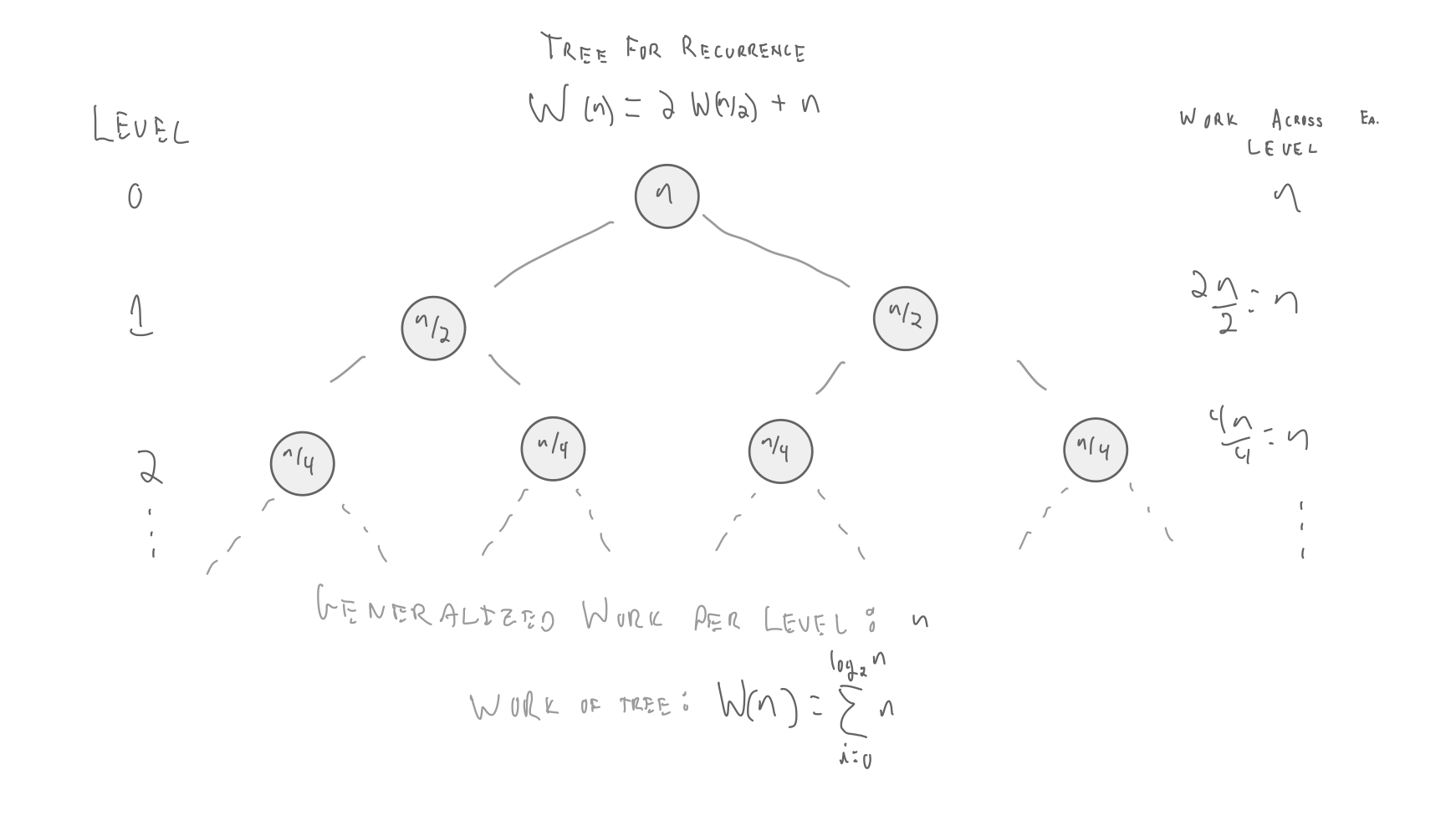
$C(\hbox{root}) = n$
$C(\hbox{level}\:1) = \Big(\frac{n}{2}\Big) + \Big(\frac{n}{2}\Big) = n$
Cost has remained the same when descending one level in the tree.
So, total cost is number of levels times maximum cost per level.
- Number of levels = $\lg n$
- Maximum cost per level = $n\:\:$ (last level: $n$ leaves with cost 1 each; first level: one node with cost $n$)
- $O(n \lg n)$
Practice¶
Let's look at some examples:
$$ W(n) = 2 W(n/2) + \sqrt{n} $$$$ W(n) = 3 W(n/2) + n $$$$ W(n) = 2 W(n/3) + n $$$$ W(n) = 3 W(n/3) + n $$Useful observation: If we have a recurrence of the form $W(n) = aW(n/b) + f(n)$, then the number of leaves is $O(a^{\log_b n})$, or equivalently, $O(n^{log_b a})$.
This is leaf-dominated, so it is $O(n)$.
$$ W(n) = 3 W(n/2) + n $$This is leaf-dominated, so it is $O(n^{\log_2 3})$.
$$ W(n) = 2 W(n/3) + n $$This is root-dominated, so it is $O(n)$.
$$ W(n) = 3 W(n/3) + n $$This is balanced, so it is $O(n \log n)$.
More examples (some trickier than others):
$$ W(n) = W(n - 1) + n $$$$ W(n) = \sqrt{n} W(\sqrt{n}) + n^2 $$$$ W(n) = W(\sqrt{n}) + W(n/2) + n $$$$ W(n) = W(n/2) + W(n/3) + 1 $$This is actually a balanced recurrence since every level has the same cost and there are $n$ levels - the recurrence is $O(n^2)$.
$$ W(n) = \sqrt{n} W(\sqrt{n}) + n^2 $$This is root-dominated so it is $O(n^2)$.
$$ W(n) = W(\sqrt{n}) + W(n/2) + n $$This is root-dominateed so it is $O(n)$.
$$ W(n) = W(n/2) + W(n/3) + 1 $$This recurrence is a little tricky - while it is leaf-dominated we need to calculate the number of leaves. The book has a derivation of this.