CMPS 2200¶

Introduction to Algorithms¶

Parallelism¶

Agenda:

Motivate why we are using parallel algorithms
Overview of how to analyze parallel algorithms

What is parallelism? (aka parallel computing)¶

ability to run multiple computations at the same time

Why study parallel algorithms?¶

faster
lower energy usage
- performing a computation twice as fast sequentially requires roughly eight times as much energy
- energy consumption is a cubic function of clock frequency
better hardware now available
- multicore processors are the norm
- GPUs (graphics processor units)

E.g., more than one million core machines now possible:
SpiNNaker (Spiking Neural Network Architecture), University of Manchester

Example: Summing a list¶

Summing can easily be parallelised by splitting the input list into two (or $k$) pieces.

In [5]:

def sum_list(mylist):
    result = 0
    for v in mylist:
        result += v
    return result

sum_list(range(8))

Out[5]:

becomes

In [16]:

from multiprocessing.pool import ThreadPool

def parallel_sum_list(mylist):
    result1, result2 = in_parallel(
        sum_list, mylist[:len(mylist)//2],
        sum_list, mylist[len(mylist)//2:]
    )
    # combine results
    return result1 + result2

def in_parallel(f1, arg1, f2, arg2):
    with ThreadPool(2) as pool:
        result1 = pool.apply_async(f1, [arg1])  # launch f1
        result2 = pool.apply_async(f2, [arg2])  # launch f2
        return (result1.get(), result2.get())   # wait for both to finish

parallel_sum_list(list(range(10)))

Out[16]:

How much faster should parallel version be?
How much energy is consumed?

parallel_sum_list is twice as fast sum_list with same amount of energy

...almost. This ignores the overhead to setup parallel code and communicate/combine results.

$O(\frac{n}{2}) + O(1)$
$O(1)$ to combine results

some current state-of-the-art results:

application	sequential	parallel (32 core)	speedup
sort $10^7$ strings	2.9	.095	30x
remove duplicated from $10^7$ strings	.66	.038	17x
min. spanning tree for $10^7$ edges	1.6	.14	11x
breadth first search for $10^7$ edges	.82	.046	18x

The speedup of a parellel algorithm $P$ over a sequential algorithms $S$ is: $$ speedup(P,S) = \frac{T(S)}{T(P)} $$

Parallel software¶

So why isn't all software parallel?

dependency

The fundamental challenge of parallel algorithms is that computations must be independent to be performed in parallel. Parallel computations should not depend on each other.

What should this code output?

In [ ]:

total = 0

def count(size):
    global total
    for _ in range(size):
        total += 1
    
def race_condition_example():
    global total
    in_parallel(count, 1000000,
                count, 1000000)
    print(total)
    
race_condition_example()

Counting in parallel is hard!¶

motivates functional programming (next class)

This course will focus on:

understanding when things can run in parallel and when they cannot
algorithm, not hardware specifics (though see CMPS 4760: Distributed Systems)
runtime analysis

Analyzing parallel algorithms¶

work: total number of primitive operations performed by an algorithm

For sequential machine, just total sequential time.
On parallel machine, work is divided among $P$ processors

perfect speedup: dividing $W$ work across $P$ processors yields total time $\frac{W}{P}$

span: longest sequence of dependencies in computation

time to run with an infinite number of processors

measure of how "parallelized" an algorithm is

also called: critical path length or computational depth

Intuition¶

work: total operations performed by a computation

span: minimum possible time that the computation requires

work: $T_1$ = time using one processor

span: $T_\infty$ = time using $\infty$ processors

We would still require span time even if we had as many processors as we could use

parallelism = $\frac{T_1}{T_\infty}$

maximum possible speedup with unlimited processors

What is work and span of parallel_sum_list algorithm using $n$ threads?

In [8]:

def in_parallel_n(tasks):
    """
    generalize in_parallel for n threads.
    
    Params:
      tasks: list of (function, argument) tuples to run in parallel
      
    Returns:
      list of results
    """
    with ThreadPool(len(tasks)) as pool:
        results = []
        for func, arg in tasks:
            results.append(pool.apply_async(func, [arg]))
        return [r.get() for r in results]


def parallel_n_sum_list(mylist):
    results = in_parallel_n([ (sum_list, [v]) for v in mylist ])
    # combine results...looks familiar...
    result = 0
    for v in results:
        result += v
    return result

parallel_n_sum_list(range(8))

Out[8]:

work: $O(n)$

span: $O(n)$

oops that didn't work...

can we do better?

the problem:

The combination step happened in serial

idea:

parallelize combination steps
implement recursive solution where each thread returns the sum of its part of the problem
- We'll have threads summing results in parallel

strategy:

divide the problem in half at each step
recursively sum each half
combine the results (by adding the two sums together)

divide and conquer¶

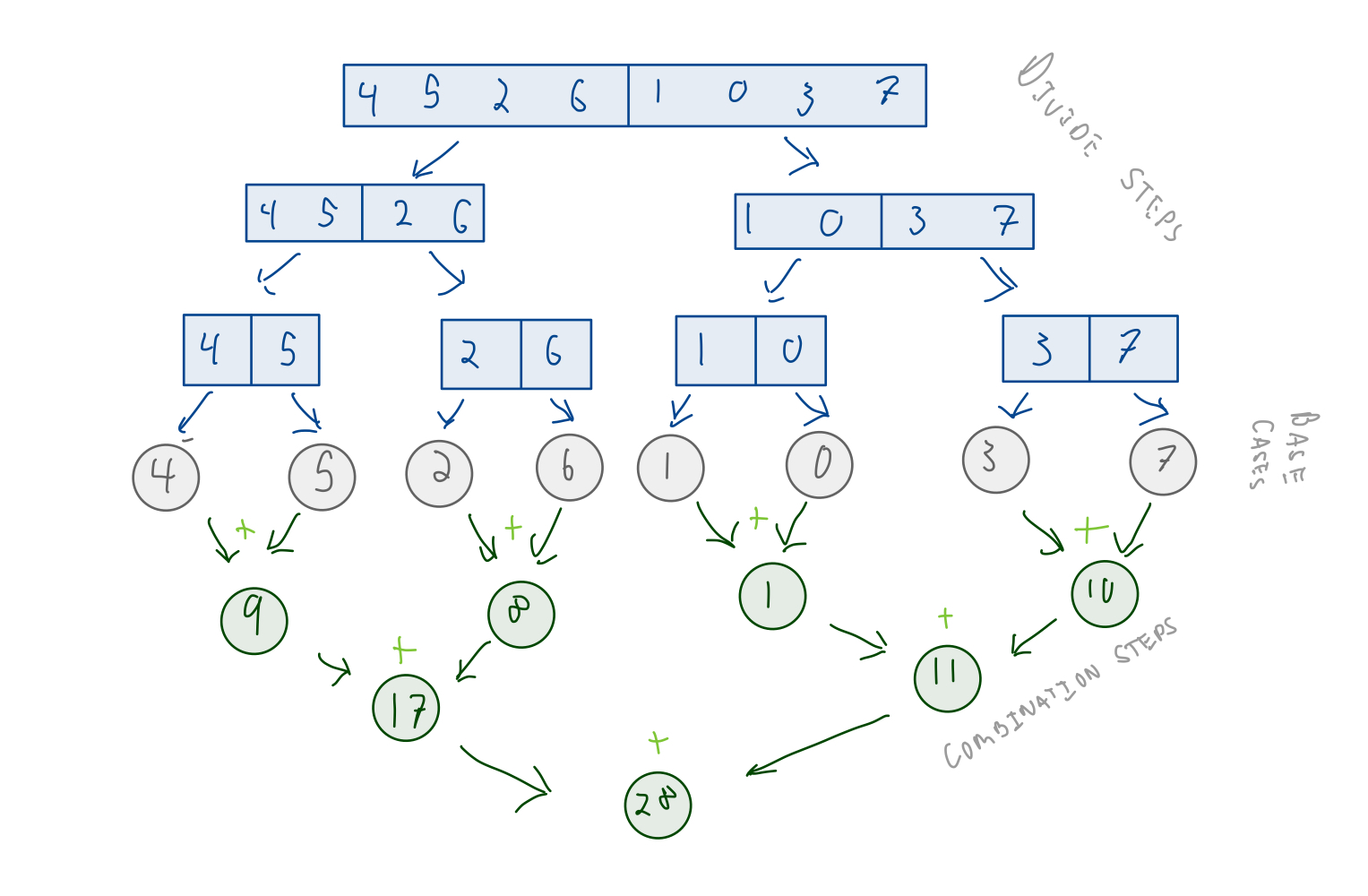
Implementation¶

In [11]:

# recursive, serial
def sum_list_recursive(mylist):    
    if len(mylist) == 1:
        return mylist[0]

    left_sum = sum_list_recursive(mylist[:len(mylist)//2])
    right_sum = sum_list_recursive(mylist[len(mylist)//2:])
    
    return left_sum + right_sum

sum_list_recursive(range(8))

Out[11]:

In [15]:

# recursive, parallel
def sum_list_recursive_parallel(mylist):    
    if len(mylist) == 1:
        return mylist[0]
    
    # each thread spawns more threads
    left_sum, right_sum = in_parallel(
        sum_list_recursive_parallel, mylist[:len(mylist)//2],
        sum_list_recursive_parallel, mylist[len(mylist)//2:]
    )
    return left_sum + right_sum

sum_list_recursive_parallel(range(8))

Out[15]:

In [ ]:

from multiprocessing.pool import ThreadPool

def in_parallel(f1, arg1, f2, arg2):
    with ThreadPool(2) as pool:
        result1 = pool.apply_async(f1, [arg1])  # launch f1
        result2 = pool.apply_async(f2, [arg2])  # launch f2
        return (result1.get(), result2.get())   # wait for both to finish

Computation Graph¶

This is a Directed-acyclic graph (DAG) where

Each node is a unit of computation
Each edge is a computational dependency
- Edge from node $A$ and $B$ means $A$ must complete before $B$ begins

Computation Graph: Work and Span¶

work: total number of operations performed over all nodes

span: longest sequence of dependent operations in computation

Our First Recursive Analysis¶

So, what is work and span for sum_list_recursive_parallel?

work: total work done across all recursive calls
span: length of longest path

How many recursive calls are there?

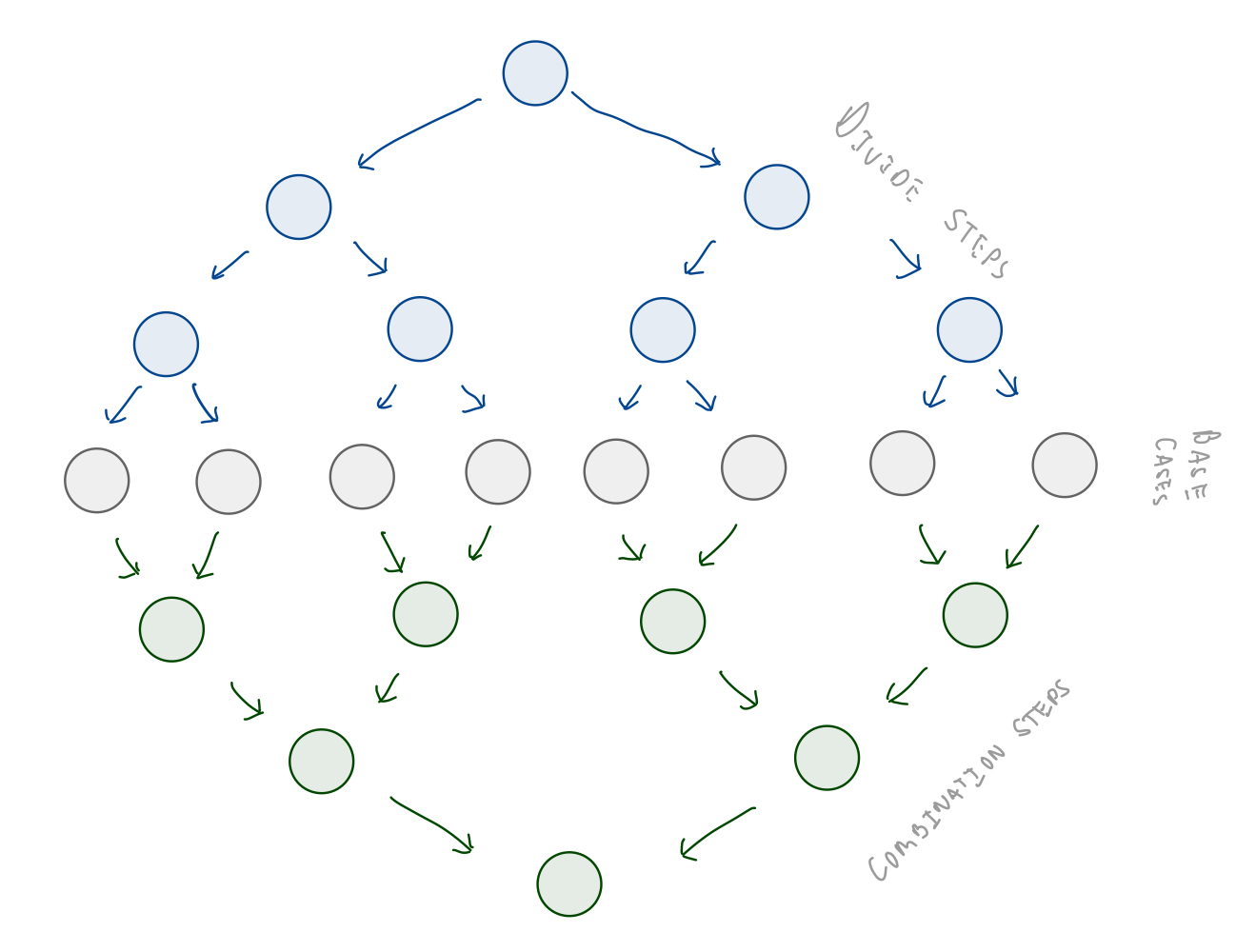
The number of recursive call is the number of nodes in the divide and base cases part of the computation graph.

This is a perfect binary tree.

How many nodes are in a perfect binary tree?

$2\cdot\hbox{num_leaves} - 1$

Our First Recursive Analysis continued...¶

Number of recursive calls: $2\cdot\hbox{num_leaves} - 1$

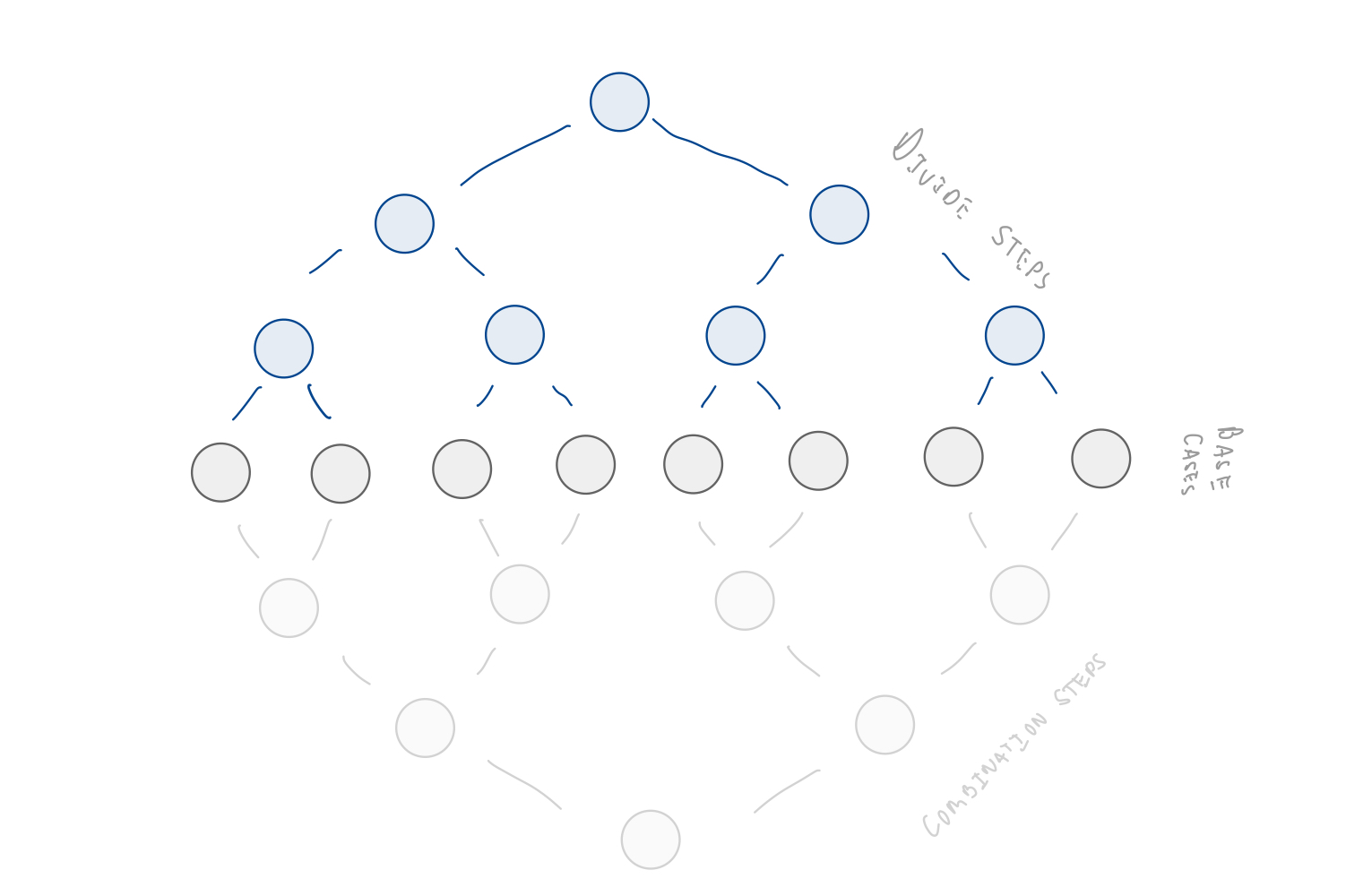
How many leaves are there?

$2^h$ where $h$ is the height of the tree.

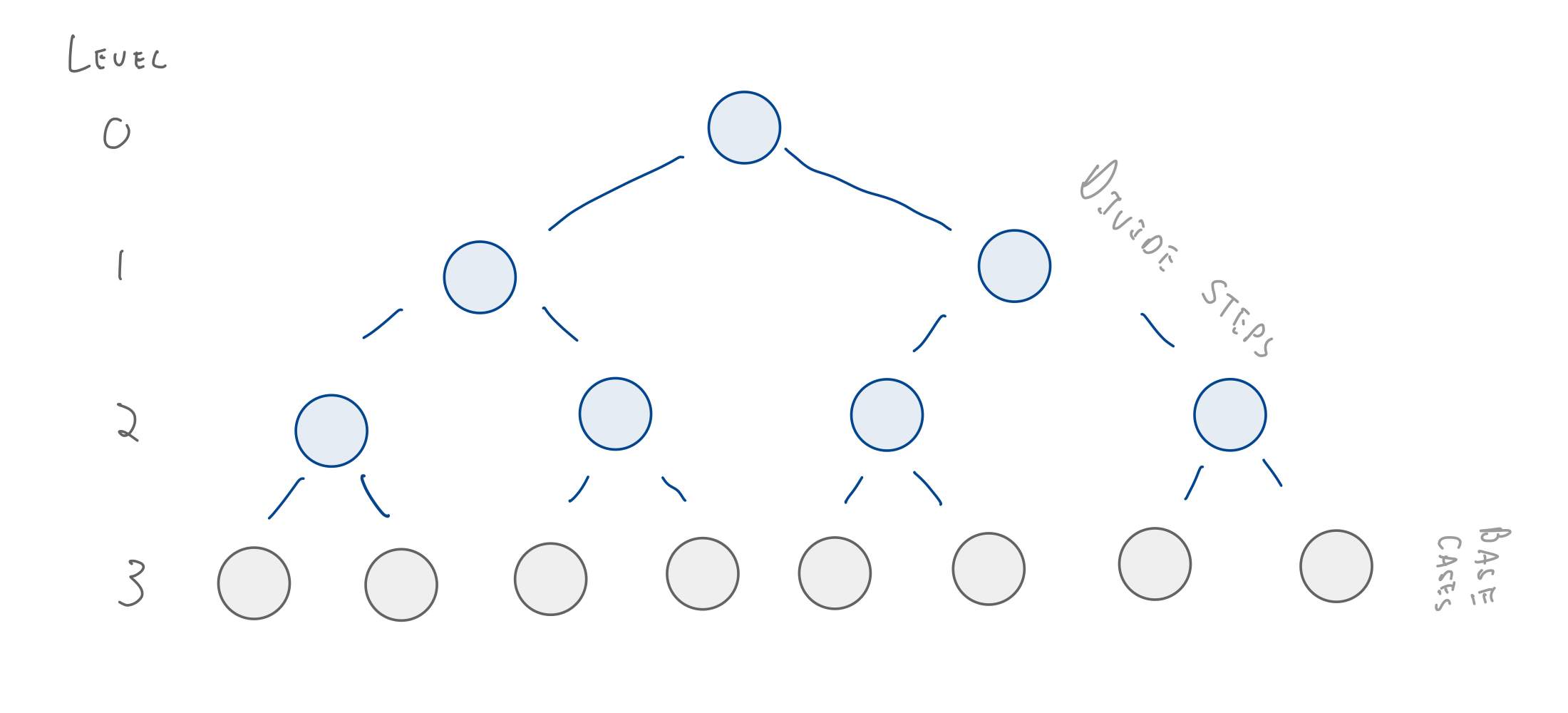
height: the number of edges between the root and bottom most leaf

What is the height of a perfect binary tree with $n$ nodes?

$O(\log_2 n)$

Our First Recursive Analysis: Work¶

work: total number of operations performed over all recursive calls

Number recursive calls: $2\cdot\hbox{num_leaves}-1$

$$2\cdot2^{(\log_2 n)} - 1 = 2n - 1$$

How much work is performed within each recursive call?

In [ ]:

def sum_list_recursive(mylist):    
    if len(mylist) == 1:
        return mylist[0]

    left_sum = sum_list_recursive(mylist[:len(mylist)//2])
    right_sum = sum_list_recursive(mylist[len(mylist)//2:])
    
    return left_sum + right_sum

$O(1)$

We have $2n-1$ recursive calls, each requiring $O(1)$ work.

so,

work: $2n-1 \in O(n)$

Our First Recursive Analysis: Span¶

span: longest sequence of dependent operations in computation

The longest chain of dependent operations is twice the height of a perfect binary tree.

span: $2 \log_2 n \in O(\log_2 n)$

Our First Recursive Analysis: Pulling it all together¶

work: total number of operations performed over all recursive calls
span: longest sequence of dependent operations in computation

work: $O(n)$
span: $O(\log_2 n)$

What about parallelism?

parallelism = $\frac{T_1}{T_\infty} = \frac{\texttt{work}}{\texttt{span}}$

parallelism: $O(\frac{n}{\log_2 n})$

exponential speedup!

Work Efficiency¶

A parallel algorithm is (asymptotically) work efficient if the work is asymptotically the same as the time for an optimal sequential algorithm that solves the same problem.

Since $T_{\hbox{sequential}} = T_1 = O(n)$, our parallel algorithm is work efficient

Using $p$ processors¶

Of course, we don't have $\infty$ processors. What if we only have $p$?

It can be justified that:

$T_p \leq \frac{\texttt{work}}{p} + \texttt{span}$
$T_p \in O(\frac{\texttt{work}}{p} + \texttt{span})$

So, assuming $\log_2 n$ processors, our parallel sum algorithm has time

$O(\frac{n}{\log_2 n} + \log_2 n)$

compared to $O(n)$ of serial algorithm.

In our analyses throughout this course, we'll consider the work, span, and parallelism of our algorithms, not the number of processors available.

Amdahl's Law¶

As seen above, some parts of parallel algorithms are sequential.

We expect that the bigger the "sequential" part of the parallel algorithm is, the lower its speedup.

How bad is a little bit of sequential code?

Let $T_1$ be the total time of the parallel algorithm on one processor (aka the work). Let's set this value to 1.
Let $S$ be the amount of time that cannot be parallelized.
Assume (generously) that the remaining time (1-S) gets perfect speedup using $p$ processors.
Then we have

$T_1 = S + (1-S) = 1$
$T_P = S + \frac{(1-S)}{p}$

Amdahl's Law¶

$$\frac{T_1}{T_p} = \frac{1}{S + \frac{1 − S}{p}}$$

speedup using $p$ processors is limited by the fraction of the algorithm that is parallelizable.

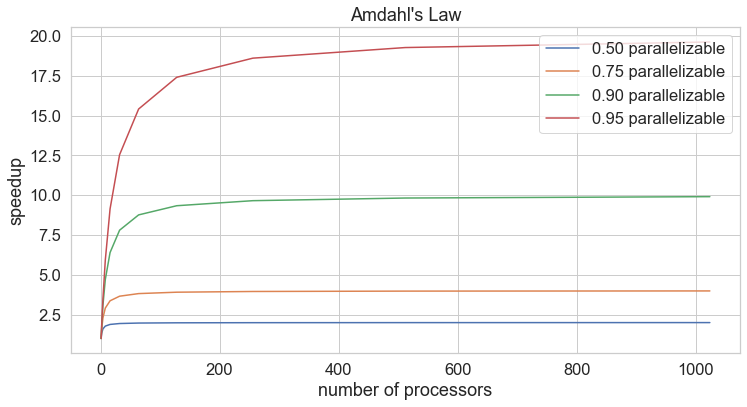
If 95% of the program can be parallelized, the theoretical maximum speedup using parallel computing would be 20 times.

If 50% of the program can be parallelized, the theoretical maximum speedup using parallel computing would be 2 times.

even if you have a billion processors!

Reasons for hope:

As number of processors grow, span becomes more important than work.
scalability matters more than performance
we can tradeoff work and span in algorithm choice

Key Points¶

We can parallelize algorithms by running recursive calls in their own threads.

The work of a recursive parallel algorithm is the total number of operations across all recursive calls.

The span of a recursive parallel algorithm is the longest chain of dependent operations.

Coming up¶

Next we will discuss functional languages to adopt some key ideas to make designing and implementing parallel algorithms easy.